Question

【题目】已知中，边的长与边上的高的和为，当面积最大时，则其周长的最小值为________（用含的代数式表示）．

Answer 1

【答案】

【解析】

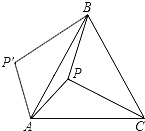
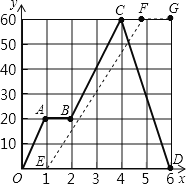
设BC上的高为x，则BC=a﹣x，△ABC的面积为S，S=x（a﹣x），根据二次函数的顶点坐标，可得出x的值，过点A作直线l∥BC，再作出点B关于直线l的对称点E，连接CE，交l于点F，可得△CBE是直角三角形，根据勾股定理求出CE的长，从而得出周长的最小值．

设BC上的高为x．

∵边BC的长与BC边上的高的和为a，∴BC=a﹣x，设△ABC的面积为S，∴S=x（a﹣x）=﹣x2+ax．

∵当△ABC面积最大时，∴x=a，∴BC=a，过点A作直线l∥BC，再作出点B关于直线l的对称点E，连接CE，交l于点F，当点A与点F重合时，△ABC周长的最小值，∴BG=GE=AD=a，∴BE=a．

∵直线l∥BC，∴∠EBC=∠EGA=90°，∴CE==a，∴△ABC的最小周长=a．

故答案为：a．