题目内容
【题目】已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β.
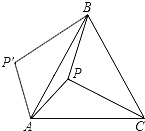
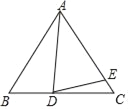
(1)如图,若点D在线段BC上,点E在线段AC上.
①如果∠ABC=60°,∠ADE=70°,那么α= °,β= °;
②求α,β之间的关系式.
(2)请直接写出不同于以上②中的α,β之间的关系式可以是 .(写出一个即可.)
【答案】(1)①20, 10;②α=2β; (2)α=2β﹣180°或α=180°﹣2β.
【解析】
(1)①先利用等腰三角形的性质求出∠DAE,进而求出∠BAD,即可得出结论;
②利用等腰三角形的性质和三角形的内角和即可得出结论;
(2)①当点E在CA的延长线上,点D在线段BC上,同(1)的方法即可得出结论;②当点E在CA的延长线上,点D在CB的延长线上,同(1)的方法即可得出结论.
(1)①∵AB=AC,∠ABC=60°,
∴∠BAC=60°,
∵AD=AE,∠ADE=70°,
∴∠DAE=180°﹣2∠ADE=40°,
∴α=∠BAD=60°﹣40°=20°,
∴∠ADC=∠BAD+∠ABD=60°+20°=80°,
∴β=∠CDE=∠ADC﹣∠ADE=10°,
故答案为:20,10;
②设∠ABC=x,∠AED=y,
∴∠ACB=x,∠AED=y,
在△DEC中,y=β+x,
在△ABD中,α+x=y+β=β+x+β,
∴α=2β;
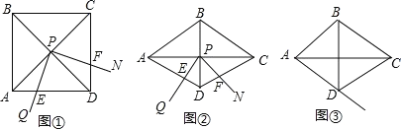
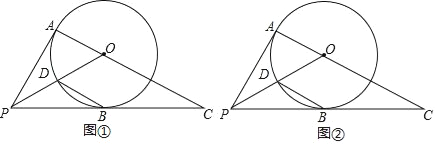
(2)①当点E在CA的延长线上,点D在线段BC上,
如图1
设∠ABC=x,∠ADE=y,
∴∠ACB=x,∠AED=y,
在△ABD中,x+α=β﹣y,
在△DEC中,x+y+β=180°,
∴α=2β﹣180°,
②当点E在CA的延长线上,点D在CB的延长线上,
如图2,同①的方法可得α=180°﹣2β.
故答案为:α=2β﹣180°或α=180°﹣2β.