题目内容
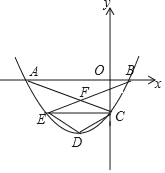
【题目】如图,抛物线y=mx2+2mx+n经过A(﹣3,0),C(0,﹣![]() )两点,与x轴交于另一点B.
)两点,与x轴交于另一点B.
(1)求经过A,B,C三点的抛物线的解析式;
(2)过点C作CE∥x轴交抛物线于点E,写出点E的坐标,并求AC、BE的交点F的坐标
(3)若抛物线的顶点为D,连结DC、DE,四边形CDEF是否为菱形?若是,请证明;若不是,请说明理由.
【答案】(1)y=![]() x2+x﹣
x2+x﹣![]() ;(2)F点坐标为(﹣1,﹣1);(3)四边形CDEF是菱形.证明见解析
;(2)F点坐标为(﹣1,﹣1);(3)四边形CDEF是菱形.证明见解析
【解析】
将A、C点的坐标代入抛物线的解析式中,通过联立方程组求得该抛物线的解析式;
根据(1)题所得的抛物线的解析式,可确定抛物线的对称轴方程以及B、C点的坐标,由CE∥x轴,可知C、E关于对称轴对称。根据A、C点求得直线AC的解析式,根据B、E点求出直线BE的解析式,联立方程求得的解,即为F点的坐标;
由E、C、F、D的坐标可知DF和EC互相垂直平分,则可判定四边形CDEF为菱形.
(1)∵抛物线y=mx2+2mx+n经过A(﹣3,0),C(0,﹣![]() )两点,
)两点,
∴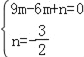 ,解得
,解得![]() ,
,
∴抛物线解析式为y=![]() x2+x﹣
x2+x﹣![]() ;
;
(2)∵y=![]() x2+x﹣
x2+x﹣![]() ,
,
∴抛物线对称轴为直线x=﹣1,
∵CE∥x轴,
∴C、E关于对称轴对称,
∵C(0,﹣![]() ),
),
∴E(﹣2,﹣![]() ),
),
∵A、B关于对称轴对称,
∴B(1,0),
设直线AC、BE解析式分别为y=kx+b,y=k′x+b′,
则由题意可得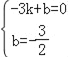 ,
,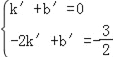 ,
,
解得![]() ,
,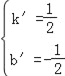 ,
,
∴直线AC、BE解析式分别为y=﹣![]() x﹣
x﹣![]() ,y=
,y=![]() x﹣
x﹣![]() ,
,
联立两直线解析式可得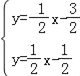 ,解得
,解得![]() ,
,
∴F点坐标为(﹣1,﹣1);
(3)四边形CDEF是菱形.
证明:∵y=![]() x2+x﹣
x2+x﹣![]() =
=![]() (x+1)2﹣2,
(x+1)2﹣2,
∴D(﹣1,﹣2),
∵F(﹣1,﹣1),
∴DF⊥x轴,且CE∥x轴,
∴DF⊥CE,
∵C(0,﹣![]() ),且F(﹣1,﹣1),D(﹣1,﹣2),
),且F(﹣1,﹣1),D(﹣1,﹣2),
∴DF和CE互相平分,
∴四边形CDEF是菱形.