题目内容
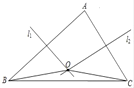
【题目】如图,已知四边形ABCD是平行四边形,小慧同学利用直尺和规进行了如下操作:①连接AC,分别以点A、C为圆心,以大于![]() AC的长为半径画弧,两弧相交于点P、Q;②作直线PQ,分别交BC、AC、AD于点E、O、F,连接AE、CF.根据操作结果,解答下列问题:
AC的长为半径画弧,两弧相交于点P、Q;②作直线PQ,分别交BC、AC、AD于点E、O、F,连接AE、CF.根据操作结果,解答下列问题:
(1)线段AF与CF的数量关系是 .
(2)若∠BAD=120°,AE平分∠BAD,AB=8,求四边形AECF的面积.

【答案】(1)FA=FC;(2)![]()
【解析】
(1)根据基本作图和线段垂直平分线的性质进行判断;
(2))由AE平分∠BAD得到∠BAE=∠DAE=![]() ∠BAD=60°,利用平行四边形的性质得AD∥BC,则∠AEB=∠DAE=60°,所以△ABE为等边三角形,则AE=AB=8,∠B=60°,于是可计算出AC=
∠BAD=60°,利用平行四边形的性质得AD∥BC,则∠AEB=∠DAE=60°,所以△ABE为等边三角形,则AE=AB=8,∠B=60°,于是可计算出AC=![]() AB=8
AB=8![]() ,再证明△AEF为等边三角形得到EF=8,然后根据三角形面积公式利用四边形AECF的面积=
,再证明△AEF为等边三角形得到EF=8,然后根据三角形面积公式利用四边形AECF的面积=![]() EF×AC进行计算.
EF×AC进行计算.
解:(1)由作法得EF垂直平分AC,
所以FA=FC.
故答案为FA=FC;
(2)∵AE平分∠BAD,
∴∠BAE=∠DAE=![]() ∠BAD=60°,
∠BAD=60°,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠AEB=∠DAE=60°,
∴△ABE为等边三角形,
∴AE=AB=8,∠B=60°,
∵EA=EC,
∴∠EAC=∠ECA=![]() ∠AEB=30°,
∠AEB=30°,
∴AC=![]() AB=8
AB=8![]() ,
,
∵∠CAD=60°-30°=30°,
即OA平分∠EAF,
∴AF=AE=8,
∴△AEF为等边三角形,
∴EF=8,
∴四边形AECF的面积=![]() .
.

【题目】某新店开业宣传,进店有礼活动,店员们需准备制作圆柱体礼品纸盒(如图①),每个纸盒由1个长方形侧面和2个圆形底面组成,现有100张正方形纸板全部以A或者B方法截剪制作(如图②),设截剪时x张用A方法.

(1)根据题意,完成以下表格:
裁剪法A | 裁剪法B | |
长方形侧面 | x |
|
圆形底面 |
| 0 |
(2)若裁剪出的长方形侧面和圆形底面恰好用完,问能做多少个纸盒?
(3)按以上制作方法,若店员们希望准备300个礼盒,那至少还需要正方形纸板 张.