题目内容
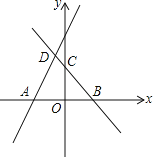
【题目】如图,直线y=![]() x+m与x轴交于点A(-3,0),直线y=-x+2与x轴、y轴分别交于B、C两点,并与直线y=
x+m与x轴交于点A(-3,0),直线y=-x+2与x轴、y轴分别交于B、C两点,并与直线y=![]() x+m相交于点D,
x+m相交于点D,
(1)点D的坐标为 ;
(2)求四边形AOCD的面积;
(3)若点P为x轴上一动点,当PD+PC的值最小时,求点P的坐标.
【答案】(1)(-1,3);(2)![]() ;(3) (-
;(3) (-![]() ,0).
,0).
【解析】
(1)把A、B的坐标代入函数解析式,求出函数解析式,即可求出D点的坐标;
(2)根据面积公式求出面积即可;
(3)找出P点的位置,求出直线EC的解析式,即可求出PD点的坐标.
解:(1)把A(-3,0)代入y=![]() x+m,得m=
x+m,得m=![]() ,
,
∵直线y=-x+2与x轴、y轴分别交于B、C两点,
∴B点坐标为(2,0),C(0,2),
解方程组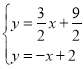 得:
得:![]() ,
,
∴D点坐标为(-1,3);
故答案为:(-1,3);
(2)∵直线y=-x+2与x轴、y轴分别交于B、C两点,
∴B点坐标为(2,0),C(0,2),
∴四边形AOCD的面积=S△DAB-S△COB
=![]() ×5×3-
×5×3-![]() ×2×2
×2×2
=![]() ;
;
(3)作D关于x轴的对称点E,连接CE,交x轴于P,此时PD+PC的值最小,
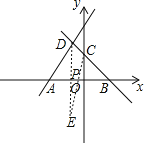
∵D点坐标为(-1,3),
∴E点的坐标为(-1,-3),
设直线CE的解析式为y=ax+b,
把E、C的坐标代入得:![]()
解得:a=5,b=2,
即直线CE的解析式为y=5x+2,
当y=0时,x=-![]() ,
,
即P点的坐标为(-![]() ,0).
,0).

 计算高手系列答案
计算高手系列答案【题目】“中国汉字听写大会”是由中央电视台和国家语言文字工作委员会联合主办的节目,希望通过节目的播出,能吸引更多的人关注对汉字文化的学习.某校也开展了一次“汉字听写”比赛,每位参赛学生听写40个汉字.比赛结束后随机抽取部分学生的听写结果,按听写正确的汉字个数x绘制成了以下不完整的统计图.
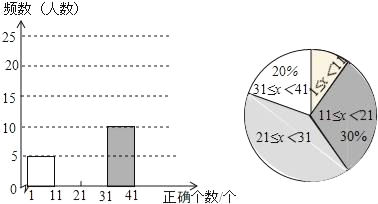
根据以上信息回答下列问题:
(1)本次共随机抽取了 名学生进行调查,听写正确的汉字个数x在 范围的人数最多;
(2)补全频数分布直方图;
(3)各组的组中值如下表所示.若用各组的组中值代表各组每位学生听写正确的汉字个数,求被调查学生听写正确的汉字个数的平均数;
听写正确的汉字个数x | 组中值 |
1≤x<11 | 6 |
11≤x<21 | 16 |
21≤x<31 | 26 |
31≤x<41 | 36 |
(4)该校共有1350名学生,如果听写正确的汉字个数不少于21个定为良好,请你估计该校本次“汉字听写”比赛达到良好的学生人数.
【题目】为鼓励市民节约用水,某市自来水公司对每户用水量进行了分段计费,每户每月用水量在规定吨数以下的收费标准相同,规定吨数以上的超过部分收费相同.如表是小明家1-4月
用水量和交费情况,根据表格提供的数据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 6 | 7 | 12 | 15 |
水费(元) | 12 | 14 | 28 | 37 |
(1)该市规定用水量为 吨,规定用量内的收费标准是 元/吨,超过部分的收费标准是 元/吨。
(2)若小明家5月份用水20吨,则应缴水费 元。
(3)若小明家6月份应交水费46元,则6月份他们家的用水量是多少吨?