题目内容
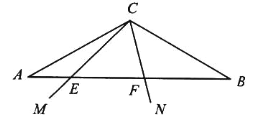
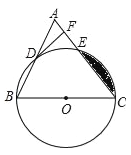
【题目】如图,已知在△ABC中,BC=AC,以BC为直径的⊙O与边AB、AC分别交于点D、E,DF⊥AC于点F.
(1)求证:点D是AB的中点;
(2)判断DF与⊙O的位置关系,并证明你的结论;
(3)若⊙O的半径为10,sinB=![]() ,求阴影部分面积.
,求阴影部分面积.
【答案】(1)证明见解析(2)DF与⊙O相切(3)![]()
【解析】
(1)连接CD,根据直径所对的圆周角为90°得∠BDC=90°,再由等腰三角形的三线合一得出结论;
(2)根据中位线的定义可以知道:OD是△ABC的中位线,则OD∥AC,因为DF⊥AC,所以DF⊥OD,得出DF与 O相切;
(3)如图3,连接OE、BE,先根据特殊的三角函数值求出∠ABC=60°,所以△ABC是等边三角形,求出直角△BEC各边的长,就可以求其面积,根据中线的性质可知△OEC的面积就是△BEC面积的-半,所求的阴影面积是扇形面积与△OEC的面积的差.
(1)连接CD
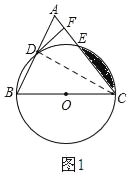
∵BC是⊙O的直径,
∴∠BDC=90°
又∵AC=BC,∴点D是AB的中点;
(2)DF与⊙O相切,
如图2,连接OD
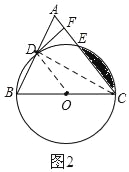
∵O是BC的中点,点D是AB的中点,
∴OD是△ABC的中位线,
∴OD∥AC
又∵DF⊥AC,
∴DF⊥OD,且OD是半径
∴DF与⊙O相切;
(3)如图3,连接OE,作OM⊥AC
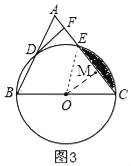
∵sin∠ABC=![]() ,
,
∴∠ABC=60°
又∵AC=BC,
∴△ABC是等边三角形
∴∠C=60°
又∵OE=OC
∴△OEC是等边三角形
∴EC=OC=10,∠EOC=60°
∵OM⊥AB,∠ACB=60°
∴MC=5,OM=![]() MC=5
MC=5![]()
∴S△OEC=![]() ×EC×OM=25
×EC×OM=25![]()
∴S阴影=S扇形OEC﹣S△OEC=![]() ﹣25
﹣25![]() =
=![]() ﹣25
﹣25![]()

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目