题目内容
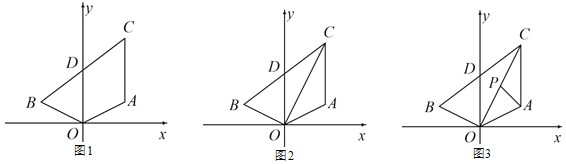
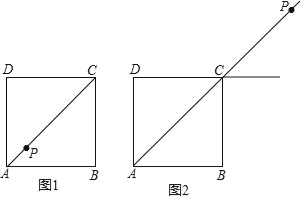
【题目】在正方形ABCD中,点P在射线AC上,作点P关于直线CD的对称点Q,作射线BQ交射线DC于点E,连接BP.
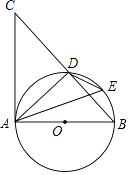
(1)当点P在线段AC上时,如图1.
①依题意补全图1;
②若EQ=BP,则∠PBE的度数为 ,并证明;
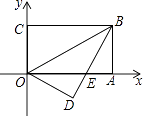
(2)当点P在线段AC的延长线上时,如图2.若EQ=BP,正方形ABCD的边长为1,请写出求BE长的思路.(可以不写出计算结果)
【答案】(1)①作图见解析;②45°(2)见解析.
【解析】
(1)①作点P关于直线CD的对称点Q,作射线BQ交射线DC于点E,连接BP;②依据题意得到DP=EP,再根据四边形内角和求得∠BPE=90°,根据BP=EP,即可得到∠PBE=45°;
(2)连接PD,PE,依据△CPD≌△CPB,可得DP=BP,∠1=∠2,根据DP=EP,可得∠3=∠1,进而得到∠PEB=45°,∠3=∠4=22.5°,△BCE中,已知∠4=22.5°,BC=1,可求BE长.
解:(1)①作图如下:
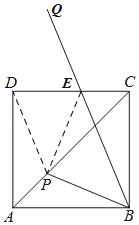
②如图,连接PD,PE,易证△CPD≌△CPB,
∴DP=BP,∠CDP=∠CBP,
∵P、Q关于直线CD对称,
∴EQ=EP,
∵EQ=BP,
∴DP=EP,
∴∠CDP=∠DEP,
∵∠CEP+∠DEP=180°,
∴∠CEP+∠CBP=180°,
∵∠BCD=90°,
∴∠BPE=90°,
∵BP=EP,
∴∠PBE=45°,
故答案为:45°;
(2)思路:如图,连接PD,PE,

易证△CPD≌△CPB,
∴DP=BP,∠1=∠2,
∵P、Q关于直线CD对称,
∴EQ=EP,∠3=∠4,
∵EQ=BP,
∴DP=EP,
∴∠3=∠1,
∴∠3=∠2,
∴∠5=∠BCE=90°,
∵BP=EP,
∴∠PEB=45°,
∴∠3=∠4=22.5°,
在△BCE中,已知∠4=22.5°,BC=1,可求BE长.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
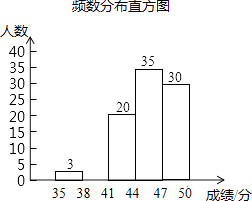
小学生10分钟应用题系列答案【题目】为了传承优秀传统文化,我市组织了一次初三年级1200名学生参加的“汉字听写”大赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(满分50分),整理得到如下的统计图表:
成绩(分) | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
人数 | 1 | 2 | 3 | 3 | 6 | 7 | 5 | 8 | 15 | 9 | 11 | 12 | 8 | 6 | 4 |
成绩分组 | 频数 | 频率 |
35≤x<38 | 3 | 0.03 |
38≤x<41 | a | 0.12 |
41≤x<44 | 20 | 0.20 |
44≤x<47 | 35 | 0.35 |
47≤x≤50 | 30 | b |
请根据所提供的信息解答下列问题:
(1)样本的中位数是分;
(2)频率统计表中a= , b=;
(3)请补全频数分布直方图;
(4)请根据抽样统计结果,估计该次大赛中成绩不低于41分的学生有多少人?