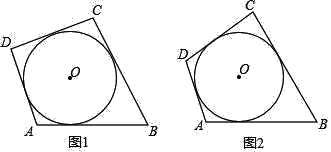题目内容
【题目】如图1是甲、乙两个圆柱形水槽的轴截面示意图.乙槽中有一圆柱形铁块放在其中(圆柱形铁块的下底面完全落在水槽底面上),现将甲槽中的水匀速注人乙槽.甲、乙两个水槽中水的深度![]() 与注水时间
与注水时间![]() (分钟)之间的关系如图2所示.根据图象提供的信息,解答下列问题:
(分钟)之间的关系如图2所示.根据图象提供的信息,解答下列问题:
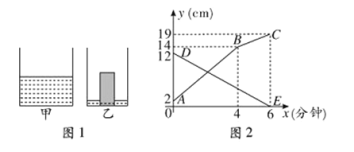
(1)图2中折线![]() 表示 槽中的水的深度与注水时间的关系,线段
表示 槽中的水的深度与注水时间的关系,线段![]() 表示 槽中的水的深度与注水时间的关系(填“甲”或“乙”),点
表示 槽中的水的深度与注水时间的关系(填“甲”或“乙”),点![]() 的纵坐标表示的实际意义是 ;
的纵坐标表示的实际意义是 ;
(2)当![]() 时,分别求出
时,分别求出![]() 和
和![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)注水多长时间时,甲、乙两个水槽中的水深度相同?
(4)若乙槽底面积为![]() 平方厘米(壁厚不计) ,求乙槽中铁块的体积.
平方厘米(壁厚不计) ,求乙槽中铁块的体积.
【答案】(1)乙;甲;乙槽中圆柱形铁块的高度是14厘米;(2)y甲=-2x+12,y乙=3x+2;(3)注水2分钟;(4)84cm3
【解析】
(1)根据题目中甲槽向乙槽注水可以得到折线ABC是乙槽中水的深度与注水时间之间的关系,点B表示的实际意义是乙槽内液面恰好与圆柱形铁块顶端相平;
(2)根据题意分别求出两个水槽中y与x的函数关系式即可;
(3)根据(2)中y与x的函数关系式,令y相等即可得到水位相等的时间;
(4)用水槽的体积减去水槽中水的体积即可得到铁块的体积;
解:(1)由题意可得:
∵乙槽中含有铁块,
∴乙槽中水深不是匀速增长,
∴折线![]() 表示乙槽中水深与注水时间的关系,
表示乙槽中水深与注水时间的关系,
线段DE表示甲槽中水深与注水时间的关系,
由点B的坐标可得:
点B的纵坐标表示的实际意义是:乙槽中圆柱形铁块的高度是14厘米;
故答案为:乙;甲;乙槽中圆柱形铁块的高度是14厘米;
(2)设线段AB、DE的解析式分别为:y甲=k1x+b1,y乙=k2x+b2,
∵AB经过点(0,2)和(4,14),DE经过(0,12)和(6,0),
∴ ,
,
解得:![]() ,
,
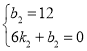 ,
,
解得: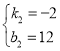 ,
,
∴当![]() 时, y甲=-2x+12,y乙=3x+2;
时, y甲=-2x+12,y乙=3x+2;
(3)由(2)可知:
令y甲=y乙,
即3x+2=-2x+12,
解得x=2,
∴当2分钟时两个水槽水面一样高.
(4)由图象知:当水槽中没有没过铁块时4分钟水面上升了12cm,即1分钟上升3cm,
当水面没过铁块时,2分钟上升了5cm,即1分钟上升2.5cm,
设铁块的底面积为acm2,
则乙水槽中不放铁块的体积为:2.5×36cm3,
放了铁块的体积为3×(36-a)cm3,
∴1×3×(36-a)=1×2.5×36,
解得a=6,
∴铁块的体积为:6×14=84(cm3).

 阅读快车系列答案
阅读快车系列答案【题目】某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔 试 | 面 试 | 体 能 | |
甲 | 85 | 80 | 75 |
乙 | 80 | 90 | 73 |
丙 | 83 | 79 | 90 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分(不计其他因素条件),请你说明谁将被录用.