题目内容
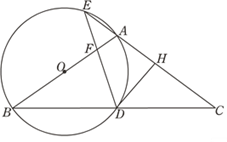
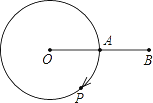
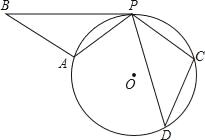
【题目】如图,已知△PDC是⊙O的内接三角形,CP=CD,若将△PCD绕点P顺时针旋转,当点C刚落在⊙O上的A处时,停止旋转,此时点D落在点B处.
(1)求证:PB与⊙O相切;
(2)当PD=2![]() ,∠DPC=30°时,求⊙O的半径长.
,∠DPC=30°时,求⊙O的半径长.
【答案】(1)详见解析;(2)2.
【解析】
(1)连接OA、OP,由旋转可得:△PAB≌△PCD,再由全等三角形的性质可知AP=PC=DC,再根据∠BPA=∠DPC=∠D可得出∠BPO=90°,进而可知PB与⊙O相切;
(2)过点A作AE⊥PB,垂足为E,根据∠BPA=30°,PB=2![]() ,△PAB是等腰三角形,可得出BE=EP=
,△PAB是等腰三角形,可得出BE=EP=![]() ,PA=2,PB与⊙O相切于点P可知∠APO=60°,故可知PA=2.
,PA=2,PB与⊙O相切于点P可知∠APO=60°,故可知PA=2.
(1)证明:连接OA、OP,OC,由旋转可得:△PAB≌△PCD,
∴PA=PC=DC,
∴AP=PC=DC,∠AOP=∠POC=2∠D,∠APO=∠OAP=![]() ,
,
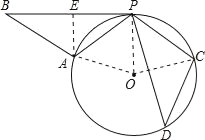
又∵∠BPA=∠DPC=∠D,
∴∠BPO=∠BPA+![]() =90°
=90°
∴PB与⊙O相切;
(2)解:过点A作AE⊥PB,垂足为E,
∵∠BPA=30°,PB=2![]() ,△PAB是等腰三角形;
,△PAB是等腰三角形;
∴BE=EP=![]() ,
,
PA=![]() =
=![]() =2
=2
又∵PB与⊙O相切于点P,
∴∠APO=60°,
∴OP=PA=2.

练习册系列答案
相关题目