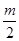题目内容
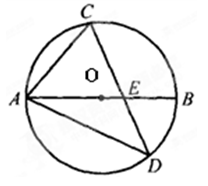
如下图,四边形OABC为菱形,点A、B在以点O为圆心的弧DE上,OA=3,
∠1=∠2, 则扇形ODE的面积为 .
∠1=∠2, 则扇形ODE的面积为 .

3
分析:连接OB.根据等边三角形的性质可以求得∠AOC=120°,再结合∠1=∠2,即可求得扇形所在的圆心角的度数,从而根据扇形的面积公式进行求解.
解答:解:连接OB.
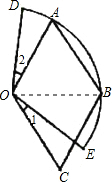
∵OA=OB=OC=AB=BC,
∴∠AOB+∠BOC=120°.
又∠1=∠2,
∴∠DOE=120°.
∴扇形ODE的面积为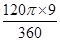 =3π.
=3π.
解答:解:连接OB.

∵OA=OB=OC=AB=BC,
∴∠AOB+∠BOC=120°.
又∠1=∠2,
∴∠DOE=120°.
∴扇形ODE的面积为
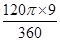 =3π.
=3π.
练习册系列答案
相关题目
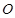 是以数轴的原点
是以数轴的原点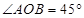 ,点
,点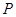 (P与O不重合)在数轴上运动,若过点
(P与O不重合)在数轴上运动,若过点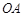 平行的直线与⊙
平行的直线与⊙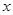 ,则
,则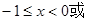
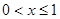
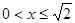
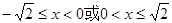
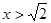
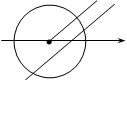
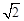 ,若在⊙O上找一点C,使AC=
,若在⊙O上找一点C,使AC=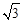 ,则∠BAC= ▲ °.
,则∠BAC= ▲ °.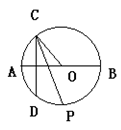
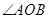 的度数为
的度数为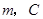 是ACB上一点,
是ACB上一点, D、E是AB上不同的两点(不与A、B两点重合),则
D、E是AB上不同的两点(不与A、B两点重合),则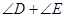 的度数为( )
的度数为( )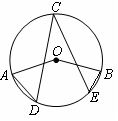
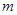 B.
B.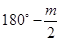 C.
C.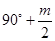 D.
D.