题目内容
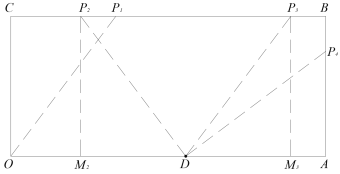
【题目】如图,已知在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C、D的坐标分别为A(9,0)、C(0,4),D(5,0),点P从点O出发,以每秒1个单位长度的速度沿O→C→B→A运动,点P的运动时间为t秒.则当t=____秒时,△ODP是腰长为5的等腰三角形?
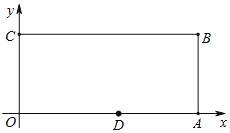
【答案】6或7或12或14
【解析】
当OP=OD时,可得P1点;当DP=OD时,可得P2、P3、P4三种情况,再运用勾股定理可分别求解.
解:当OP=OD时,可得P1点,此时由勾股定理可得,OC2+CP12=OP12,即42+CP12=52,解得CP1=3,则t=![]() 秒;
秒;
当DP=OD时,可得P2、P3、P4三种情况,当P点运动到P2位置时,作P2M2⊥OA,由勾股定理可得,P2M22+ DM22=DP22,即42+ DM22=52,解得DM2=3,同理可解得DM3=AP4=3,
故,当P点运动到P2位置时,t=![]() 秒;当P点运动到P3位置时,t=
秒;当P点运动到P3位置时,t=![]() 秒;当P点运动到P4位置时,t=
秒;当P点运动到P4位置时,t=![]() 秒;
秒;
故答案为:6或7或12或14.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目