题目内容
【题目】如图1，已知抛物线y=﹣ 
x2﹣ 
x+c与x轴相交于A、B两点（B点在A点的左侧），与y轴相交于C点，且AB=10．
（1）求这条抛物线的解析式；
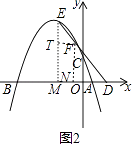
（2）如图2，D点在x轴上，且在A点的右侧，E点为抛物线上第二象限内的点，连接ED交抛物线于第二象限内的另外一点F，点E到y轴的距离与点F到y轴的距离之比为3：1，已知tan∠BDE= 
，求点E的坐标；
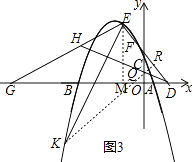
（3）如图3，在（2）的条件下，点G由B出发，沿x轴负方向运动，连接EG，点H在线段EG上，连接DH，∠EDH=∠EGB，过点E作EK⊥DH，与抛物线相应点E，若EK=EG，求点K的坐标．
【答案】
（1）解：由y=﹣ 
x2﹣ 
x+c，
可得对称轴为x=﹣4
∵AB=10，
∴点A的坐标为（1，0），
∴ 
，
∴c=3
∴抛物线的解析式为y=﹣ 
+3．
（2）解：如图2，作EM⊥x轴，垂足为点M，FN⊥x轴，垂足为点N，FT⊥EM，垂足为点T．
∴∠TMN=∠FNM=∠MTF=90°，
∴四边形FTMN为矩形，
∴EM∥FN，FT∥BD．
∴∠BDE=∠EFT，
∵tan∠BDE= 
，
∴tan∠EFT= ，
设E（﹣3m，yE），F（﹣m，yF）
∴ 
∵y=﹣ +3过点E、F，
则yE﹣yF= 
=（﹣3m2+8m+3）﹣（﹣ 
+3），
解得m=0（舍去）或m=1，
当m=1时，﹣3m=﹣3，
∴ 
=8．
∴E（﹣3，8）
（3）解：如图3，作EM⊥x轴，垂足为点M，过点K作KR⊥ED，与ED相交于点R，与x轴相交于点Q．
∵∠KER+∠EDH=90°，∠EGM+∠GEM=90°，∠EDH=∠EGM，
∴∠KER=∠GEM，
在△EGM和△EKR中，
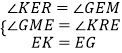
∴△EGM≌△EKR，
∴EM=ER=8，
∵tan∠BDE= ．
∴ED=10，
∴DR=2，
∴DQ= 
∴Q（﹣ ，0），
可求R（ 
， 
）
∴直线RQ的解析式为：y= 
．
设点K的坐标为（x， ）代入抛物线解析式可得x=﹣11
∴K（﹣11，﹣8）．
【解析】（1）利用抛物线的轴对称性，求出对称轴，结合AB=10，求出A点坐标代入即可；（2）设出E的横坐标，表示 出E、F的纵坐标，利用tan∠BDE的定义构建关于m的方程，求出E的坐标；（3）通过作垂线构造出全等三角形，即△EGM≌△EKR，求出直线RQ解析式，解出二者联立的方程组， 即可求出其与抛物线交点坐标.
