题目内容
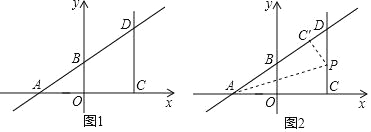
【题目】已知:如图1,在平面直角坐标系中,一次函数y=![]() x+3交x轴于点A,交y轴于点B,点C是点A关于y轴对称的点,过点C作y轴平行的射线CD,交直线AB与点D,点P是射线CD上的一个动点.
x+3交x轴于点A,交y轴于点B,点C是点A关于y轴对称的点,过点C作y轴平行的射线CD,交直线AB与点D,点P是射线CD上的一个动点.
(1)求点A,B的坐标.
(2)如图2,将△ACP沿着AP翻折,当点C的对应点C′落在直线AB上时,求点P的坐标.
(3)若直线OP与直线AD有交点,不妨设交点为Q(不与点D重合),连接CQ,是否存在点P,使得S△CPQ=2S△DPQ,若存在,请求出对应的点Q坐标;若不存在,请说明理由.
【答案】(1)A(﹣4,0),B(0,3);(2)P(4,![]() );(3)满足条件的点Q(12,12)或(
);(3)满足条件的点Q(12,12)或(![]() ,4).
,4).
【解析】
令x=0,y=0即可求出A,B坐标.
因为点C是点A关于y轴对称的点,求得C坐标,因为CD⊥x轴,所以求得D坐标,由折叠知,AC'=AC,所以C'D=AD﹣AC',设PC=a,在Rt△DC'P中通过勾股定理求得a值,即可求得P点坐标.
在S△CPQ=2S△DPQ情况下分类讨论P点坐标即可求解.
解:(1)令x=0,则y=3,
∴B(0,3),
令y=0,则![]() x+3=0,
x+3=0,
∴x=﹣4,
∴A(﹣4,0);
(2)∵点C是点A关于y轴对称的点,
∴C(4,0),
∵CD⊥x轴,
∴x=4时,y=6,∴D(4,6),
∴AC=8,CD=6,AD=10,
由折叠知,AC'=AC=8,
∴C'D=AD﹣AC'=2,
设PC=a,
∴PC'=a,DP=6﹣a,
在Rt△DC'P中,a2+4=(6﹣a)2,
∴a=![]() ,
,
∴P(4,![]() );
);
(3)设P(4,m),
∴CP=m,DP=|m﹣6|,
∵S△CPQ=2S△DPQ,
∴CP=2PD,
∴2|m﹣6|=m,
∴m=4或m=12,
∴P(4,4)或P(4,12),
∵直线AB的解析式为y=![]() x+3①,
x+3①,
当P(4,4)时,直线OP的解析式为y=x②,
联立①②解得,x=12,y=12,
∴Q(12,12),
当P(4,12)时,直线OP解析式为y=3x③,
联立①③解得,x=![]() ,y=4,
,y=4,
∴Q(![]() ,4),
,4),
即:满足条件的点Q(12,12)或(![]() ,4).
,4).

 阅读快车系列答案
阅读快车系列答案