��Ŀ����
����Ŀ����һ����·��˳����A��B��C���أ��ס�������ͬʱ��A�س������ֱ�����ǰ��B�أ�C�أ��׳�����B��ͣ��һ��ʱ���ԭ��ԭ·���أ��ҳ�����C�غ�����ԭ��ԭ·���أ��ҳ��ȼ׳���1Сʱ����A�أ��ס�������������ʻ��·��y��ǧ�ף���ʱ��x��ʱ��������������ʱ��ʼ��ʱ��֮���ͼ����ͼ��ʾ��
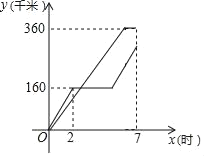
��1���������仯�����У��Ա������� ������������� ����
��2���ҳ���ʻ���ٶ�Ϊ�� ��ǧ��/Сʱ��
��3���׳�����B��ͣ���˶�ã�B����C��֮��ľ���Ϊ����ǧ�ף�
���𰸡���1��x��y����2��60����3���׳�����B��ͣ����3Сʱ��B����C��֮��ľ���Ϊ20ǧ�ף�
��������
��1�����ݺ��������Ϻ���ͼ��õ��Ա�����x���������y��
��2��������֪����֪�ҳ��ȼ׳���1Сʱ����ʻ6Сʱ�������·�̳���ʱ�伴�ɵõ��ٶȣ�
��3������ʱ��7Сʱ��ȥ����2Сʱ�õ��׳�ͣ����ʱ�䣬���ҳ���A��ʻ��C�صõ�A��C֮���·�̣��ټ�ȥ�׳���ʻ��A��B֮���·�̼��ɵõ�B��C֮���·��.
�⣺��1����ͼ��ɵã�
�Ա�����x���������y��
�ʴ�Ϊ��x��y��
��2���ҳ���ʻ���ٶ�Ϊ��360����7��1����60ǧ��/Сʱ��
�ʴ�Ϊ��60��
��3���׳�����B��ͣ���ˣ�7����2+2����3��Сʱ����
B����C��֮��ľ���Ϊ��360��2��160��20��ǧ�ף���
�𣺼׳�����B��ͣ����3Сʱ��B����C��֮��ľ���Ϊ20ǧ�ף�