题目内容
【题目】如图,矩形AEFG的顶点E,G分别在正方形ABCD的AB,AD边上,连接B,交EF于点M,交FG于点N,设AE=a,AG=b,AB=c(b<a<c).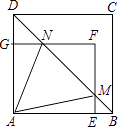
(1)求证: ![]() =
= ![]() ;
;
(2)求△AMN的面积(用a,b,c的代数式表示);
(3)当∠MAN=45°时,求证:c2=2ab.
【答案】
(1)证明:过点N作NH⊥AB于点H,过点M作MI⊥AD于点I,
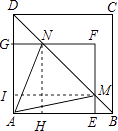
∵四边形ABCD是正方形,
∴∠ADB=∠ABD=45°,
∴△NHB和△DIM是等腰直角三角形,四边形AGNH和四边形AEMI是矩形,
∴BN= ![]() NH=
NH= ![]() AG=
AG= ![]() b,DM=
b,DM= ![]() MI=
MI= ![]() AE=
AE= ![]() a,
a,
∴ ![]() =
= ![]()
(2)解:S△AMN=S△ABD﹣S△ABM﹣S△ADN
= ![]() ABAD﹣
ABAD﹣ ![]() ABME﹣
ABME﹣ ![]() ADNG
ADNG
= ![]() c2﹣
c2﹣ ![]() c(c﹣a)﹣
c(c﹣a)﹣ ![]() c(c﹣b)
c(c﹣b)
= ![]() c(c﹣c+a﹣c+b)
c(c﹣c+a﹣c+b)
= ![]() c(a+b﹣c)
c(a+b﹣c)
(3)解:∵∠DMA=∠ABD+∠MAB=∠MAB+45°,∠BAN=∠MAB+∠MAN=∠MAB+45°,
∴∠DMA=∠BAN,
∵∠ABD=∠ADB=45°,
∴△ADM∽△NBA,
∴ ![]() =
= ![]() ,
,
∵DM= ![]() a,BN=
a,BN= ![]() b,
b,
∴c2=2ab.
【解析】(1)作NH⊥AB垂足为H,作MI⊥AD垂足为I,依据题意可得到△NHB和△DIM是等腰直角三角形,四边形AGNH和四边形AEMI是矩形,则可求得BN=![]() b,DM=
b,DM=![]() a,最后,代入计算即可;
a,最后,代入计算即可;
(2)依据图形可知S△AMN=S△ABD-S△ABM-S△ADN,故此可得到S△AMN=![]() c2-
c2-![]() c(c-a)-
c(c-a)-![]() c(c-b),最后进行整理即可;
c(c-b),最后进行整理即可;
(3)首先证明∠DMA=∠BAN,然后再由∠ABD=∠ADB=45°可得到△ADM∽△NBA,最后,依据相似三角形的性质列出比例式求解即可.
【考点精析】本题主要考查了相似三角形的判定与性质的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.