题目内容
【题目】如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1 ,它与x轴交于两点O,A;将C1绕点A旋转180°得到C2 , 交x轴于A1;将C2绕点A1旋转180°得到C3 , 交x轴于点A2 . .....如此进行下去,直至得到C2018 , 若点P(4035,m)在第2018段抛物线上,则m的值为________.
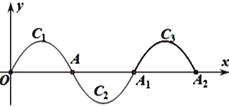
【答案】-1
【解析】
每次变化时,开口方向变化但形状不变,则 ![]() ,故开口向上时a=1,开口向下时a=-1;与x轴的交点在变化,可发现规律抛物线Cn与x轴交点的规律是(2n-2,0)和(2n,0),由两点式
,故开口向上时a=1,开口向下时a=-1;与x轴的交点在变化,可发现规律抛物线Cn与x轴交点的规律是(2n-2,0)和(2n,0),由两点式![]() 求得解析式,把x=4035代入解析式,即可求得m的值.
求得解析式,把x=4035代入解析式,即可求得m的值.
由抛物线C1:y=-x(x-2),
令y=0,∴-x(x-2)=0,解得 ![]()
∴与x轴的交点为O(0,0),A(2,0).
抛物线C2的开口向上,且与x轴的交点为∴A(2,0)和A1(4,0),
则抛物线C2:y= (x-2)(x-4);
抛物线C3的开口向下,且与x轴的交点为∴A1(4,0)和A2(6,0),
则抛物线C3:y= -(x-4)(x-6);
抛物线C4的开口向上,且与x轴的交点为∴A2(6,0)和A3(8,0),
则抛物线C4:y=(x-6)(x-8);
同理:
抛物线C2018的开口向上,且与x轴的交点为∴A2016(4034,0)和A2017(4036,0),
则抛物线C2018:y=(x-4034)(x-4036);
当x=4035时,y= 1×(-1)-1.
故答案为:-1.

练习册系列答案
相关题目