题目内容
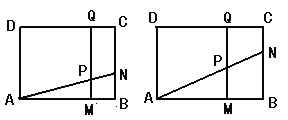
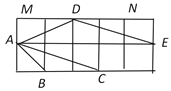
【题目】如图,在2×2的正方形网格中,小正方形的边长均为1,△ABC与△ADE的顶点都在格点上.
(1)求证:△ABC∽△ADE;
(2)求∠MDA+∠NDE的度数.
【答案】(1)证明见解析;(2) 45°.
【解析】
(1)先利用勾股定理计算出△ABC与△ADE的所有边长,则![]() ,于是根据相似三角形的判定方法即可得到△ADE∽△ABC;
,于是根据相似三角形的判定方法即可得到△ADE∽△ABC;
(2)正方形的性质可得∠1=180°-∠ABC=45°,由等角的补角相等可得∠MDA+∠NDE=∠1=45°.
(1)证明:∵AB=![]() ,AC=
,AC=![]() =
=![]() ,BC=2,AD=
,BC=2,AD=![]() =
=![]() ,DE=
,DE=![]() =
=![]() ,AE=5,
,AE=5,
∴![]() ,
,![]() ,
,![]() ,
,
∴△ADE∽△ABC;
(2)如图:
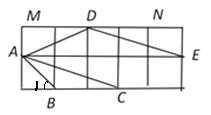
由正方形的性质得∠1=180°-∠ABC=45°,
∵△ABC∽△ADE,
∴∠ABC=∠ADE,
∴∠MDA+∠NDE=∠1=45°.

练习册系列答案
相关题目