Question

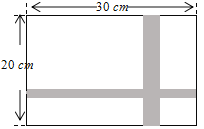
【题目】某小区为了改善居住环境，准备修建一个巨型花园ABCD，为了节约材料并种植不同花卉，决定花园一边靠墙，三边用栅栏围住，中间用一段垂直于墙的栅栏隔成两块．已知所用栅栏的总长为60米，墙长为30米，设花园垂直于墙的一边的长为米．

（1）若平行于墙的一边长为米，直接写出与的函数关系式及自变量的取值范围；

（2）当为何值时，这个矩形花园的面积最大？最大值为多少？（栅栏占地面积忽略不计）

（3）当这个花园的面积不小于288平方米时，试结合函数图象，直接写出的取值范围

Answer 1

【答案】（1）y= -3x+60（10≤x＜20）；（2）当x=10时花园面积最大，为300平方米；（3）10≤x≤12

【解析】

（1）由题意可知栅栏的总长60米可以看做有BC，AB，CD和EF四段组成，把已知数据代入即可求出y和x的函数关系；

（2）利用矩形的面积公式：长×宽和（1）的结论即可得到S和x的关系式，再利用二次函数的性质即可求出当x为何值时，这个矩形花园的面积最大和其最大值；

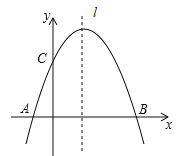
（3）由（2）可知函数的关系式，由此关系式画出函数的图象，结合图象可直接写出x的取值范围．

解：如图：

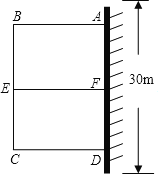
（1）∵AB+CD+EF+BC=60，AB=EF=CD=x，BC=y，

∴3x+y=60，

∴y=-3x+60（10≤x＜20）；

（2）∵S=xy=x（-3x+60），

∴S=-3x2+60x，

∵a=-3＜0，

∴当x=时，S有最大值=300平方米；

（3）∵这个花园的面积不小288平方米，

∴-3x2+60x≥288，
∴-3x2+60x-288≥0．

设y=-3x2+60x-288≥0．

此函数的图象如图所示：

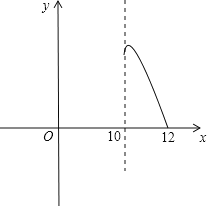
∴当这个花园的面积不小288平方米时，出x的取值范围是：10≤x≤12．