题目内容
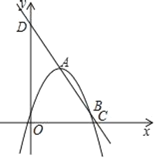
【题目】如图所示,二次函数y=k(x﹣1)2+2的图象与一次函数y=kx﹣k+2的图象交于A、B两点,点B在点A的右侧,直线AB分别与x、y轴交于C、D两点,其中k<0.
(1)求A、B两点的横坐标;
(2)若△OAB是以OA为腰的等腰三角形,求k的值;
(3)二次函数图象的对称轴与x轴交于点E,是否存在实数k,使得∠ODC=2∠BEC,若存在,求出k的值;若不存在,说明理由.
【答案】(1)1,2;(2)﹣1或﹣2或﹣3;(3)存在,![]() 或
或![]() .
.
【解析】
(1)将二次函数与一次函数联立得:k(x﹣1)2+2=kx﹣k+2,然后求解进一步得出答案即可;
(2)分两种情况:①OA=AB;②OA=OB,据此分类讨论即可;
(3)分两种情况:①当点B在x轴上方时;②当点B在x轴下方时,据此分类讨论即可.
解:(1)将二次函数与一次函数联立得:k(x﹣1)2+2=kx﹣k+2,
解得:x=1或2,
故点A、B的坐标横坐标分别为1和2;
(2)OA=![]() ,
,
①当OA=AB时,
即:1+k2=5,解得:k=±2(舍去2);
②当OA=OB时,
4+(k+2)2=5,解得:k=﹣1或﹣3;
故k的值为:﹣1或﹣2或﹣3;
(3)存在,理由:
①当点B在x轴上方时,
过点B作BH⊥AE于点H,将△AHB的图形放大见右侧图形,
过点A作∠HAB的角平分线交BH于点M,过点M作MN⊥AB于点N,过点B作BK⊥x轴于点K,
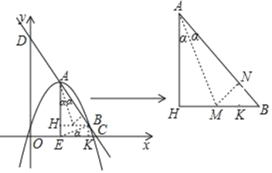
图中:点A(1,2)、点B(2,k+2),则AH=﹣k,HB=1,
设: HM=m=MN,则BM=1﹣m,
则AN=AH=﹣k,AB=![]() ,NB=AB﹣AN,
,NB=AB﹣AN,
由勾股定理得:MB2=NB2+MN2,
即:(1﹣m)2=m2+(![]() +k)2,
+k)2,
解得:m=﹣k2﹣k![]() ,
,
在△AHM中,tanα=![]() =
=![]() =k+
=k+![]() =tan∠BEC=
=tan∠BEC=![]() =k+2,
=k+2,
解得:k=![]() ,
,
此时k+2>0,则﹣2<k<0,故:舍去正值,
故k=﹣![]() ;
;
②当点B在x轴下方时,
同理可得:tanα=![]() =
=![]() =k+
=k+![]() =tan∠BEC=
=tan∠BEC=![]() ==-(k+2),
==-(k+2),
解得:k=![]() 或
或![]() ,
,
此时k+2<0,k<﹣2,故舍去![]() ,
,
故k的值为:﹣![]() 或
或![]() .
.