题目内容
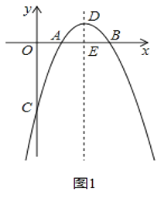
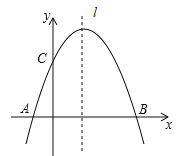
【题目】二次函数![]() 图象如图所示,下列结论:①
图象如图所示,下列结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() ;④
;④![]() ;⑤若
;⑤若![]() ,且
,且![]() ,则
,则![]() .其中正确的有______.
.其中正确的有______.
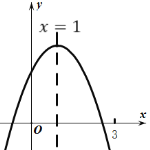
【答案】②③⑤
【解析】
根据抛物线开口方向得a<0,由抛物线对称轴为直线x=![]() =1,得到b=2a>0,即2a+b=0,由抛物线与y轴的交点位置得到c>0,所以abc<0;根据二次函数的性质得当x=1时,函数有最大值a+b+c,则当m≠1时,a+b+c>am2+bm+c,即a+b>am2+bm;根据抛物线的对称性得到抛物线与x轴的另一个交点在(1,0)的右侧,则当x=1时,y<0,所以ab+c<0;把ax12+bx1=ax22+bx2先移项,再分解因式得到(x1x2)[a(x1+x2)+b]=0,而x1≠x2,则a(x1+x2)+b=0,即x1+x2=
=1,得到b=2a>0,即2a+b=0,由抛物线与y轴的交点位置得到c>0,所以abc<0;根据二次函数的性质得当x=1时,函数有最大值a+b+c,则当m≠1时,a+b+c>am2+bm+c,即a+b>am2+bm;根据抛物线的对称性得到抛物线与x轴的另一个交点在(1,0)的右侧,则当x=1时,y<0,所以ab+c<0;把ax12+bx1=ax22+bx2先移项,再分解因式得到(x1x2)[a(x1+x2)+b]=0,而x1≠x2,则a(x1+x2)+b=0,即x1+x2=![]() ,然后把b=2a代入计算得到x1+x2=2.
,然后把b=2a代入计算得到x1+x2=2.
∵抛物线开口向下,
∴a<0,
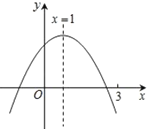
∵抛物线对称轴为直线x=![]() =1,
=1,
∴b=2a>0,即2a+b=0,所以②正确;
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①错误;
∵抛物线对称轴为直线x=1,
∴函数的最大值为a+b+c,
∴当m≠1时,a+b+c>am2+bm+c,即a+b>am2+bm,所以③正确;
∵抛物线与x轴的一个交点在(3,0)的左侧,而对称轴为直线x=1,
∴抛物线与x轴的另一个交点在(1,0)的右侧
∴当x=1时,y<0,
∴ab+c<0,所以④错误;
∵ax12+bx1=ax22+bx2,
∴ax12+bx1ax22bx2=0,
∴a(x1+x2)(x1x2)+b(x1x2)=0,
∴(x1x2)[a(x1+x2)+b]=0,
而x1≠x2,
∴a(x1+x2)+b=0,即x1+x2=![]() ,
,
∵b=2a,
∴x1+x2=2,所以⑤正确.
综上所述,正确的有②③⑤.
故答案为②③⑤.