题目内容
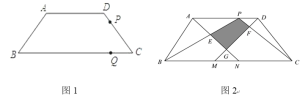
【题目】如图,已知在△ABC中,AB=AC=13,BC=10,点M是AC边上任意一点,连接MB,以MB、MC为邻边作平行四边形MCNB,连接MN,则MN的最小值是______
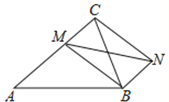
【答案】![]()
【解析】
设MN与BC交于点O,连接AO,过点O作OH⊥AC于H点,根据等腰三角形的性质和勾股定理可求AO和OH长,若MN最小,则MO最小即可,而O点到AC的最短距离为OH长,所以MN最小值是2OH.
解:设MN与BC交于点O,连接AO,过点O作OH⊥AC于H点,
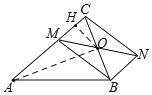
∵四边形MCNB是平行四边形,
∴O为BC中点,MN=2MO.
∵AB=AC=13,BC=10,
∴AO⊥BC.
在Rt△AOC中,利用勾股定理可得
AO=![]() =12.
=12.
利用面积法:AO×CO=AC×OH,
即12×5=13×OH,解得OH=![]() .
.
当MO最小时,则MN就最小,O点到AC的最短距离为OH长,
所以当M点与H点重合时,MO最小值为OH长是![]() .
.
所以此时MN最小值为2OH=![]() .
.
故答案为:![]() .
.

【题目】某中学初三年级积极推进走班制教学.为了了解一段时间以来,“至善班”的学习效 果,年级组织了多次定时测试,现随机选取甲、乙两个“至善班”,从中各抽取![]() 名同学在某一次定时测试中的数学成绩,其结果记录如下:
名同学在某一次定时测试中的数学成绩,其结果记录如下:
收集数据:
“至善班”甲班![]() 的名同学的数学成绩统计(满分为 100 分)(单位:分)
的名同学的数学成绩统计(满分为 100 分)(单位:分)
![]()
![]()
“至善班”乙班的![]() 名同学的数学成绩统计(满分为 100 分)(单位:分)
名同学的数学成绩统计(满分为 100 分)(单位:分)
![]()
![]()
整理数据:(成绩得分用![]() 表示)
表示)
分数 数量 班级 |
|
|
|
|
|
甲班(人数) | 1 | 3 | 4 | 6 | 6 |
乙班(人数) | 1 | 1 | 8 | 6 | 4 |
分析数据,并回答下列问题:
![]() 完成下表:
完成下表:
平均数 | 中位数 | 众数 | |
甲班 |
|
|
|
乙班 |
|
|
|
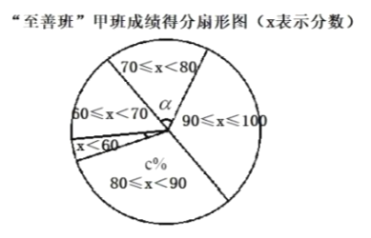
![]() 在“至善班”甲班的扇形图中, 成绩在
在“至善班”甲班的扇形图中, 成绩在![]() 的扇形中,所对的圆心角
的扇形中,所对的圆心角![]() 的度数为 . 估计全部“至善班”的
的度数为 . 估计全部“至善班”的![]() 人中优秀人数为 人.(
人中优秀人数为 人.(![]() 分及以上为优秀).
分及以上为优秀).
![]() 根据以上数据,你认为“至善班” 班(填“甲”或“乙”)所选取做样本 的同学的学习效果更好一些,你所做判断的理由是:
根据以上数据,你认为“至善班” 班(填“甲”或“乙”)所选取做样本 的同学的学习效果更好一些,你所做判断的理由是:
①
②