题目内容
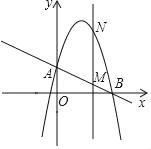
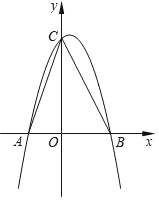
【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
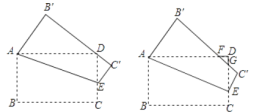
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.
【答案】(1)抛物线的解析式为y=﹣2x2+x+3;(2)∠ACB=45°;(3)D(![]() ,
, ![]() ).
).
【解析】试题分析: (1)把点A、B、C的坐标分别代入已知抛物线的解析式列出关于系数的三元一次方程组
|
,通过解该方程组即可求得系数的值;
(2)由(1)中的抛物线解析式易求点M的坐标为(0,1).所以利用待定系数法即可求得直线AM的关系式为y=
1 |
3 |
x+1.由题意设点D的坐标为(x0,
1 |
3 |
x02
2 |
3 |
x0+1),则点F的坐标为(x0,
1 |
3 |
x0+1).易求DF=
1 |
3 |
x02
2 |
3 |
x0+1(
1 |
3 |
x0+1)=
1 |
3 |
x02x0=
1 |
3 |
(x0+
3 |
2 |
)2+
3 |
4 |
.根据二次函数最值的求法来求线段DF的最大值;
(3)需要对点P的位置进行分类讨论:点P分别位于第一、二、三、四象限四种情况.此题主要利用相似三角形的对应边成比例进行解答.
试题解析: 由题意可知
|
.解得
|
.
∴抛物线的表达式为y=-
1 |
3 |
x2
2 |
3 |
x+1.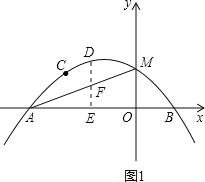
(2)将x=0代入抛物线表达式,得y=1.∴点M的坐标为(0,1).
设直线MA的表达式为y=kx+b,则
|
.
解得

练习册系列答案
相关题目