题目内容
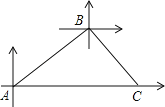
【题目】如图,在矩形纸片ABCD中,已知AB=2,BC=![]() ,点E在边CD上移动,连接AE,将多边形ABCE沿直线AE翻折得到多边形AB’C’E,点B、C的对应点分别为点B’,C’
,点E在边CD上移动,连接AE,将多边形ABCE沿直线AE翻折得到多边形AB’C’E,点B、C的对应点分别为点B’,C’
(1)当点E与点C重合时,求DF的长
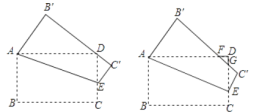
(2)如果点M为CD的中点,那么在点E从点C移动到点D的过程中,求C’M的最小值
【答案】(1) ![]() ;(2) C′M的最小值为4﹣
;(2) C′M的最小值为4﹣![]()
【解析】
(1)证明∠DCF=30°,解直角三角形即可.
(2)连接AM,AC′,MC′.求出AC′,AM,利用三角形的三边关系即可解决问题.
(1)如图,
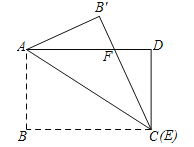
∵四边形ABCD是矩形,
∴AB=CD=2,BC=AD=2![]() ,∠B=∠BCD=∠D=90°,
,∠B=∠BCD=∠D=90°,
∴tan∠ACB=![]() ,
,
∴∠ACB=30°,
由翻折不变性可知:∠ACB=∠ACF=30°,
∠DCF=30°,
∴DF=CDtan30°=![]()
(2)如图中,连接AM,AC′,MC′.
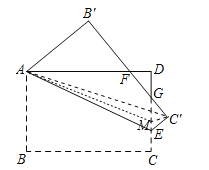
∵AC′=4,AM=![]() ,
,
∵C′M≥AC′﹣AM,
∴C′M≥4﹣![]() ,
,
∴C′M的最小值为4﹣![]() .
.

练习册系列答案
相关题目