Question

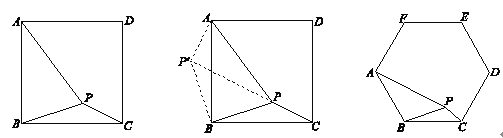
【题目】如图 1，在正方形 ABCD 中，E，F 分别是 AD，CD 上两点，BE 交 AF 于点 G，且 DE＝CF．

（1）写出 BE 与 AF 之间的关系，并证明你的结论；

（2）如图 2，若 AB＝2，点 E 为 AD 的中点，求 AG 的长度。

（3）在（2）的条件下，连接 GD，试证明 GD 是∠EGF 的角平分线，并求出 GD 的长；

Answer 1

【答案】（1）BE=AF，BE⊥AF，证明见解析；（2）；（3）证明见解析；GD=.

【解析】

（1）先判断出△BAE≌△ADF（SAS），得出BE=AF，∠ABE=∠DAF，即可得出结论；

（2）利用面积法计算即可解决问题．

（3）先利用勾股定理求出AF，进而利用面积求出DN，进而判断出AG=DN，再判断出DM=AG，即可得出GD是∠MGN的平分线，进而判断出△DGN是等腰直角三角形即可得出结论．

（1）BE=AF，BE⊥AF，理由：

四边形ABCD是正方形，

∴BA=AD=CD，∠BAE=∠D=90°，

∵DE=CF，

∴AE=DE，

∴△BAE≌△ADF（SAS），

∴BE=AF，∠ABE=∠DAF，

∵∠ABE+∠AEB=90°，

∴∠DAE+∠AEB=90°，

∴∠BGA=90°，

∴BE⊥AF．

（2）在Rt△ABE中，∵AB=2，AE=1，

∴BE=，

∵S△ABE=ABAE=BEAG，

∴．

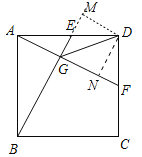
（3）如图，过点D作DN⊥AF于N，DM⊥BE交BE的延长线于M，

在Rt△ADF中，根据勾股定理得，，

∵S△ADF=AD×FD=AD×DN，

∴，

∵AG=，

∴AG=DN，

易证，△AEG≌△DEM（AAS），

∴AG=DM，

∴DN=DM，

∵DM⊥BE，DN⊥AF，

∴GD平分∠MGN，

∴∠DGN=∠MGN=45°，

∴△DGN是等腰直角三角形，

∴GD=DN=.