��Ŀ����
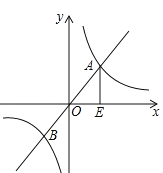
����Ŀ����ͼ����֪A(��4�� ![]() )��B��-1,2����һ�κ���y=kx+b�뷴��������y=
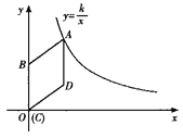
)��B��-1,2����һ�κ���y=kx+b�뷴��������y=![]() (m��0��m��0)ͼ����������㣬AC��x����C��BD��y����D��
(m��0��m��0)ͼ����������㣬AC��x����C��BD��y����D��

(1)������ͼ��ֱ�ӻش��ڵڶ������ڣ���xȡ��ֵʱ��һ�κ������ڷ�����������ֵ?
(2)����һ�κ�������ʽ��m��ֵ��
(3)��P���߶�AB�ϵ�һ�㣬����PC��PD������PCA����PDB�����ȣ����P���ꡣ
���𰸡�(1)����4��x����1��(2)��y=![]() ��m=��2��(3)����
��m=��2��(3)����![]() ��
��![]() ��
��
�����������������(1)������ͼʾֱ�ӵó��𰸣�(2)����A��B�����������һ�κ�������ʽ���k��b��ֵ������B��������뷴������������ʽ���m��ֵ��(3)�����ȸ���һ�κ��������P�����꣬���AC��OC��BD��OD�ij��ȣ�������PCA����PDB���������г�����x�ķ������x��ֵ��Ȼ��ó���P������.
���������(1)����ͼ����4��x����1ʱ��һ�κ���ֵ���ڷ�����������ֵ��
(2)����A(��4�� ![]() )��B����1��2������y=kx+b�ã�
)��B����1��2������y=kx+b�ã� 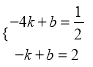 ��ã�
��ã� 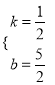
�� һ�κ����Ľ���ʽΪy=![]()
��B����1��2������y=![]() ��m=��2����m��ֵΪ��2��
��m=��2����m��ֵΪ��2��
(3)����P������Ϊ��x�� ![]() ������A��B�������֪AC=
������A��B�������֪AC=![]() ��OC=4��BD=1��OD=2��
��OC=4��BD=1��OD=2��
��֪��PCA�ĸ�Ϊx+4����PDB�ĸ�2��(![]() )����
)����![]() �ɵ�
�ɵ�
![]() �����
�����![]() ����ʱ
����ʱ![]()
�� P��������![]() ��
��![]() ��
��

 ���ĺ����Ͼ�������ϵ�д�
���ĺ����Ͼ�������ϵ�д�