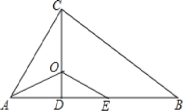
ћвƒњƒЏ»Ё
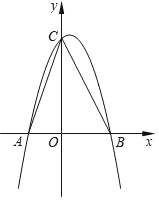
°Њћвƒњ°њ»зЌЉ£ђ“—÷™≈„ќпѕяy=©Бx2+bx+c£®b£ђc «≥£ э£©Њ≠єэA£®0£ђ2£©°ҐB£®4£ђ0£©Ѕљµг£Ѓ
£®1£©«уЄ√≈„ќпѕяµƒљвќц љЇЌґ•µг„ш±к£ї
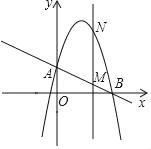
£®2£©„чіє÷±x÷бµƒ÷±ѕяx=t£ђ‘ЏµЏ“їѕуѕёљї÷±ѕяAB”ЏM£ђљї’вћх≈„ќпѕя”ЏN£ђ«уµ±t»°Їќ÷µ ±£ђMN”–„оіу÷µ£њ„оіу÷µ «ґа…ў£њ
£®3£©‘Џ£®1£©µƒ«йњцѕ¬£ђ“‘A°ҐM°ҐN°ҐDќ™ґ•µг„ч∆љ––Ћƒ±я–ќ£ђ«л÷±љ”–і≥цµЏЋƒЄцґ•µгDµƒЋщ”–„ш±к£®÷±љ”–і≥цљбєы£ђ≤ї±Ў–іљвірєэ≥ћ£©
°Њір∞Є°њ£®1£©≈„ќпѕяљвќц љќ™y=©Бx2+![]() x+2£ї≈„ќпѕяµƒґ•µг„ш±кќ™£®
x+2£ї≈„ќпѕяµƒґ•µг„ш±кќ™£®![]() £ђ
£ђ![]() £©£ї£®2£©t=2 ±£ђMN”–„оіу÷µ£ђ„оіу÷µќ™4£ї£®3£©Dµг„ш±кќ™£®0£ђ6£©їт£®0£ђ©Б2£©їт£®4£ђ4£©£Ѓ
£©£ї£®2£©t=2 ±£ђMN”–„оіу÷µ£ђ„оіу÷µќ™4£ї£®3£©Dµг„ш±кќ™£®0£ђ6£©їт£®0£ђ©Б2£©їт£®4£ђ4£©£Ѓ
°Њљвќц°њЈ÷ќц£Ї£®1£©∞—A°ҐBЅљµг„ш±кіъ»л≈„ќпѕяy=©Бx2+bx+cµ√єЎ”Џb°ҐcЈљ≥ћ„й£ђ‘тљвЈљ≥ћ„йЉіњ…µ√µљ≈„ќпѕяљвќц љ£ї»їЇу∞—“ї∞г љ≈д≥…ґ•µг љµ√µљ≈„ќпѕяµƒґ•µг„ш±к£ї
£®2£©ѕ»јы”√іэґ®ѕµ эЈ®«у≥ц÷±ѕяABµƒљвќц љќ™y=©Б![]() x+2£ђ…иN£®t£ђ©Бt2+
x+2£ђ…иN£®t£ђ©Бt2+![]() t+2£©£®0£Љt£Љ4£©£ђ‘тN£®t£ђ©Б
t+2£©£®0£Љt£Љ4£©£ђ‘тN£®t£ђ©Б![]() t+2£©£ђ‘тMN=©Бt2+
t+2£©£ђ‘тMN=©Бt2+![]() t+2©Б£®©Б
t+2©Б£®©Б![]() t+2£©£ђ»їЇујы”√ґюіќЇѓ эµƒ–‘÷ љвЊцќ ћв£ї
t+2£©£ђ»їЇујы”√ґюіќЇѓ эµƒ–‘÷ љвЊцќ ћв£ї
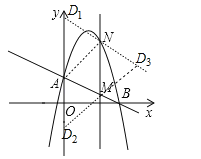
£®3£©”…£®2£©µ√N£®2£ђ5£©£ђM£®2£ђ1£©£ђ»зЌЉ£ђјы”√∆љ––Ћƒ±я–ќµƒ–‘÷ љш––ћ÷¬џ£Їµ±MNќ™∆љ––Ћƒ±я–ќµƒ±я ±£ђјы”√MN°ќAD£ђMN=AD=4ЇЌ»Јґ®ґ®“еDµг„ш±к£ђµ±MNќ™∆љ––Ћƒ±я–ќµƒґ‘љ«ѕя ±£ђјы”√AN°ќMN£ђAN=MDЇЌµг∆љ“∆µƒ„ш±кєж¬…–і≥цґ‘”¶Dµг„ш±к£Ѓ
ѕкљв£Ї£®1£©∞—A£®0£ђ2£©°ҐB£®4£ђ0£©іъ»л≈„ќпѕяy=©Бx2+bx+cµ√![]() £ђљвµ√£Ї
£ђљвµ√£Ї![]() £ђ°а≈„ќпѕяљвќц љќ™y=©Бx2+
£ђ°а≈„ќпѕяљвќц љќ™y=©Бx2+![]() x+2£ї
x+2£ї
°яy=©Бx2+![]() x+2=©Б£®x©Б
x+2=©Б£®x©Б![]() £©2+
£©2+![]() £ђ°а≈„ќпѕяµƒґ•µг„ш±кќ™£®
£ђ°а≈„ќпѕяµƒґ•µг„ш±кќ™£®![]() £©£ї
£©£ї
£®2£©…и÷±ѕяABµƒљвќц љќ™y=mx+n£ђ∞—A£®0£ђ2£©°ҐB£®4£ђ0£©іъ»лµ√£Ї![]() £ђљвµ√£Ї
£ђљвµ√£Ї £ђ°а÷±ѕяABµƒљвќц љќ™y=©Б
£ђ°а÷±ѕяABµƒљвќц љќ™y=©Б![]() x+2£ђ…иN£®t£ђ©Бt2+
x+2£ђ…иN£®t£ђ©Бt2+![]() t+2£©£®0£Љt£Љ4£©£ђ‘тN£®t£ђ©Б
t+2£©£®0£Љt£Љ4£©£ђ‘тN£®t£ђ©Б![]() t+2£©£ђ°аMN=©Бt2+
t+2£©£ђ°аMN=©Бt2+![]() t+2©Б£®©Б
t+2©Б£®©Б![]() t+2£©=©Бt2+4t =©Б£®t©Б2£©2+4£ђ
t+2£©=©Бt2+4t =©Б£®t©Б2£©2+4£ђ
µ±t=2 ±£ђMN”–„оіу÷µ£ђ„оіу÷µќ™4£ї
£®3£©”…£®2£©µ√N£®2£ђ5£©£ђM£®2£ђ1£©£ђ»зЌЉ£ђµ±MNќ™∆љ––Ћƒ±я–ќµƒ±я ±£ђMN°ќAD£ђMN=AD=4£ђ‘тD1£®0£ђ6£©£ђD2£®0£ђ©Б2£©£ђµ±MNќ™∆љ––Ћƒ±я–ќµƒґ‘љ«ѕя ±£ђAN°ќMN£ђAN=MD£ђ”…”ЏµгAѕт”“∆љ“∆2Єцµ•ќї£ђ‘ўѕт…ѕ∆љ“∆3Єцµ•ќїµ√µљNµг£ђ‘тµгMѕт”“∆љ“∆2Єцµ•ќї£ђ‘ўѕт…ѕ∆љ“∆3Єцµ•ќїµ√µљDµг£ђ‘тD3µƒ„ш±кќ™£®4£ђ4£©£Ѓ
„џ…ѕЋщ ц£ЇDµг„ш±кќ™£®0£ђ6£©їт£®0£ђ©Б2£©їт£®4£ђ4£©£Ѓ

°Њћвƒњ°њƒ≥…ћ≥°Ќђ ±єЇљшЉ„°Ґ““Ѕљ÷÷…ћ∆Јє≤200Љю£ђ∆дљшЉџЇЌ џЉџ»з±н£ђ
…ћ∆Ј√ы≥∆ | Љ„ | ““ |
љшЉџ£®‘™/Љю£© | 80 | 100 |
џЉџ£®‘™/Љю£© | 160 | 240 |
…и∆д÷–Љ„÷÷…ћ∆ЈєЇљшxЉю£ђЄ√…ћ≥° џЌк’в200Љю…ћ∆Јµƒ„№јы»уќ™y‘™£Ѓ
£®1£©«уy”лxµƒЇѓ эєЎѕµ љ£ї
£®2£©Є√…ћ∆ЈЉ∆їЃ„оґаЌґ»л18000‘™”√”ЏєЇ¬т’вЅљ÷÷…ћ∆Ј£ђ‘т÷Ѕ…ў“™єЇљшґа…ўЉюЉ„…ћ∆Ј£њ»ф џЌк’в–©…ћ∆Ј£ђ‘т…ћ≥°њ…їсµ√µƒ„оіујы»у «ґа…ў‘™£њ