题目内容
【题目】某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
(1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.
![]()
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】(1)直接根据概率公式求解即可;
(2)根据题意先画出树状图,得出所有情况数和甲、乙两位嘉宾能分为同队的结果数,再根据概率公式即可得出答案.
解:(1)∵共有三根细绳,且抽出每根细绳的可能性相同,
∴甲嘉宾从中任意选择一根细绳拉出,恰好抽出细绳AA1的概率是=![]() ;
;
(2)画树状图:
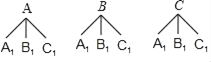
共有9种等可能的结果数,其中甲、乙两位嘉宾能分为同队的结果数为3种情况,
则甲、乙两位嘉宾能分为同队的概率是![]() .
.

练习册系列答案
相关题目