题目内容
【题目】今年的新冠疫情爆发,使很多农作物积压没法正常销售。为解决农民的困难,我市某食品加工公司主动分两次采购了一批竹笋, 第一次花费40万元,第二次花费60万元。已知第一次采购时每百千克竹笋的价格比去年的平均价格上涨了500元,第二次采购时每百千克竹笋的价格比去年的平均价格下降了500元,第二次的采购数量是第一次采购数量的两倍.
(1)试问去年每百千克竹笋的平均价格是多少元;
(2)该公司可将竹笋加工成笋干或罐头(湿笋),若单独加工成笋干,每天可加工8百千克竹笋,每百千克竹笋获利1000元; 若单独加工成罐头,每天可加工12百千克竹笋,每百千克竹笋获利600元,由于市场需要,所有采购的竹笋必需在30天内加工完毕,且加工笋干的竹笋数量不少于加工罐头的竹笋数量的一半,为获得最大利润,应将多少百千克竹笋加工成笋干?最大利润为多少.
【答案】(1)3500元;(2)为获得最大利润,应将120百千克竹笋加工成笋干,最大利润为228000元
【解析】
(1)设去年每百千克竹笋是x元,则第一次采购的平均价格为(x+500)元,第二次采购的平均价格为(x-500)元,根据第二次的采购数量是第一次采购数量的两倍,据此列方程求解;
(2)先求出今年所采购竹笋总数量,根据所有采购的竹笋必需在30天内加工完毕,加工笋干的竹笋数量不少于加工罐头的竹笋数量的一半,据此列不等式组求解,在结合利润表达式,利用一次函数的性质求出最大利润.
(1)解:设去年每百千克竹笋单价为x,则第一次单价x+500,第二次单价x-500,由题
![]() ,得x=3500
,得x=3500
经检验,x=3500是原方程的解
∴去年每百千克竹笋单价为3500元
(2)二次采购竹笋总数量为:400000÷(3500+500)+600000÷(3500-500)=300百千克
设加工成笋干的竹笋为y百千克,加工成罐头为(300-y)百千克
依题意: 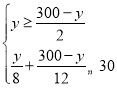
∴![]()
利润![]()
![]()
∵400>0
∴w随y增大而增大
∴当y=120时,![]() 元
元
综上,为获得最大利润,应将120百千克竹笋加工成笋干,最大利润为228000元