题目内容
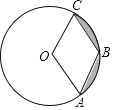
【题目】如图，在△ABC中，∠CAB＝120°，AB＝AC＝3，点E是三角形ABC 内一点，且满足
则点E 在运动过程中所形成的图形的长为 （ ）
A.
B.
C.
D.
【答案】B
【解析】
如图，将△AEC绕点A顺时针旋转120°得到△AFB，首先证明∠AFB＝120°，推出E的轨迹为圆，进而可通过弧长计算出结果．
解：将△AEC绕点A顺时针旋转120°，使得AC与AB重合，得到△AFB，连接EF，过点A作AM⊥EF，过点O作ON⊥AC
由旋转可知：AE=AF，∠EAF=120°BF=CE
∴∠AEF=∠AFE=30°
∴在Rt△AEM中，EM=
；在Rt△AFM中，MF=
∴EF=
，即
∵
∴
∴∠EFB=90°
∴∠AFB＝120°,
则∠AEC＝120°为定角所对AC＝3为定长
又因为点E在△ABC内部，
所以E的轨迹为弧GA的长度
当点E在G点时，∠CGA=120°
∴∠GOA＝60°
∴在Rt△OAN中，
∴
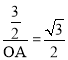，解得
所以E的轨迹长为
，
故选：B．
【题目】“垃圾分类就是新时尚”．树立正确的垃圾分类观念，促进青少年养成良好的文明习惯，对于增强公共意识，提升文明素质具有重要意义．为了调査学生对垃圾分类知识的了解情况，从甲、乙两校各随机抽取20名学生进行了相关知识测试，获得了他们的成绩（百分制，单位：分），并对数据（成绩）进行了整理、描述和分析，下面给出了部分信息．
a．甲、乙两校学生样本成绩频数分布表及扇形统计图如下：
甲校学生样本成绩频数分布表（表1）
成绩m（分） | 频数 | 频率 |
|
| 0.10 |
|
|
|
| 4 | 0.20 |
| 7 | 0.35 |
| 2 |
|
合计 | 20 | 1.0 |
b．甲、乙两校学生样本成绩的平均分、中位数、众数、方差如下表所示：（表2）
学校 | 中位数 | 众数 | 方差 | |
甲 | 76.7 | 77 | 89 | 150.2 |
乙 | 78.1 | 80 |
| 135.3 |
其中，乙校20名学生样本成绩的数据如下：
54 72 62 91 87 69 88 79 80 62 80 84 93 67 87 87 90 71 68 91
请根据所给信息，解答下列问题：
（1）表1中
___________；表2中的众数
_________；
（2）乙校学生样本成绩扇形统计图（图1）中，
这一组成绩所在扇形的圆心角度数是_________度；
（3）在此次测试中，某学生的成绩是79分，在他所属学校排在前10名，由表中数据可知该学生是________校的学生（填“甲”或“乙”），理由是________________________；
（4）若乙校1000名学生都参加此次测试，成绩80分及以上为优秀，请估计乙校成绩优秀的学生约为________人．
