题目内容
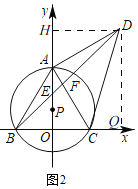
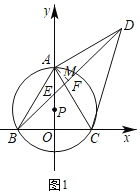
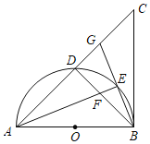
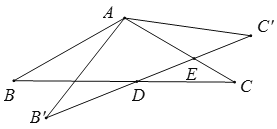
【题目】如图,点P在y轴的正半轴上,⊙P交x轴于B、C两点,交y轴于点A,以AC为直角边作等腰Rt△ACD,连接BD分别交y轴和AC于E、F两点,连接AB.
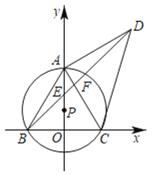
(1)求证:AB=AD;
(2)若BF=4,DF=6,求线段CD的长;
(3)当⊙P的大小发生变化而其他条件不变时,![]() 的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
【答案】(1)见解析;(2)2![]() ;(3)不发生变化,
;(3)不发生变化,![]()
【解析】
(1)先判断出△AOB≌△AOC(SAS),得出AB=AC,即可;
(2)过A作AM⊥BD于M,再判断出△ADM∽△FDA可求AD=![]() ,则CD=
,则CD=![]() ;
;
(3)不变,过D作DH⊥y轴于H,作DQ⊥x轴于Q,再证△DHA≌△AOC(AAS),得DH=AO,AH=OC,进而得出HO=BQ,所以DQ=BQ,即△DBQ为等腰直角三角形即可.
(1)证明:∵OA⊥BC,且OA过圆心点P,
∴OB=OC,
在△AOB和△AOC中,
 ,
,
∴△AOB≌△AOC(SAS),
∴AB=AC,
∵以AC为直角边作等腰Rt△ACD,
∴AD=AC,
∴AB=AD;
(2)如图1,过点A作AM⊥BD于M,
由(1)知,AB=AD,
∴DM=![]() BD,
BD,
∵BF=4,DF=6,
∴BD=10,
∴DM=5,
∵∠AMD=90°=∠DAF,∠ADM=∠FDA,
∴△ADM∽△FDA,
∴![]() ,
,
∴![]() ,
,
∴AD=![]() ,
,
在等腰直角三角形ADC中,CD=![]() AD=2
AD=2![]() ;
;
(3)![]() 的值是不发生变化,
的值是不发生变化,
理由:如图2,过点D作DH⊥y轴于H,作DQ⊥x轴于Q,
∴∠AHD=90°=∠COA,
∴∠ADH+∠DAH=90°,
∵∠CAD=90°,
∴∠CAO+∠DAH=90°,
∴∠ADH=∠CAO,
∵AD=AC,
∴△ADH≌△ACO(AAS),
∴DH=AO,AH=OC,
∵∠OHD=∠QOH=∠OQD=90°,
∴四边形OQDH是矩形,DH=OQ,DQ=OH,
又∵HO=AH+AO=OC+DH=OB+DH=OB+OQ=BQ,
∴DQ=BQ,
∴△DBQ为等腰直角三角形,
∴∠DBQ=45°,
∴∠DEH=∠BEO=45°,
∴sin∠DEH=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() ,
,
∴![]() .
.