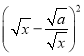题目内容
【题目】已知：在△ABC中，AB=AC，AD⊥BC于点D，分别过点A和点C作BC、AD边的平行线交于点E．
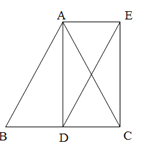
（1）求证：四边形ADCE是矩形；
（2）连结BE，若
，AD=
，求BE的长．
【答案】（1）见解析；（2）
【解析】
（1）先根据已知条件证四边形ADCE是平行四边形，再加上∠ADC=90°，证平行四边形ADCE是矩形；
（2）根据
，得到BD与AB的关系，通过解直角三角形，求AD长，则可求EC的值，在Rt△BDE中，利用勾股定理得BE.
（1）证明：∵AE // BC，CE // AD
∴ 四边形ADCE是平行四边形
∵AD ⊥BC，AB=AC
∴∠ADC=90°，
∴ 平行四边形ADCE是矩形
（2）解：连接DE,如图：
在Rt△ABD中，∠ADB =90°
∵
∴
∴设BD=x，AB=2x
∴AD=
∵AD=
∴x=2
∴BD=2
∵AB=AC，AD⊥BC
∴BC=2BD=4
∵矩形ADCE中，EC=AD=, BC=4
∴在Rt△BDE中，利用勾股定理得BE=
=
=
【题目】小明、小丽两位同学八年级10次数学单元自我检测的成绩（成绩均为整数,且个位数为0）分别如下图所示:
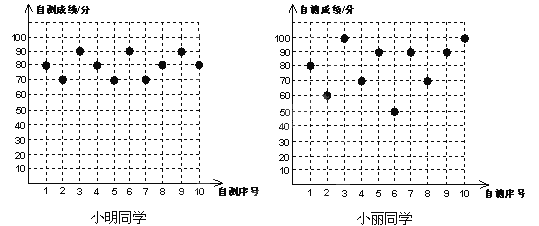
（1）根据上图中提供的数据填写下表:
平均成绩（分） | 中位数（分） | 众数（分） | 方差（S2） | |
小明 | 80 | 80 | ||
小丽 | 85 | 260 |
（2）如果将90分以上（含90分）的成绩视为优秀,则优秀率高的同学是________;
（3）根据图表信息,请你对这两位同学各提一条不超过20个字的学习建议.
【题目】瑞安市曹村镇“八百年灯会”成为温州“申遗”的宝贵项目．某公司生产了一种纪念花灯，每件纪念花灯制造成本为18元．设销售单价x（元），每日销售量y（件）每日的利润w（元）．在试销过程中，每日销售量y（件）、每日的利润w（元）与销售单价x（元）之间存在一定的关系，其几组对应量如下表所示：
（元） | 19 | 20 | 21 | 30 |
（件） | 62 | 60 | 58 | 40 |
（1）根据表中数据的规律，分别写出毎日销售量y（件），每日的利润w（元）关于销售单价x（元）之间的函数表达式．（利润＝（销售单价﹣成本单价）×销售件数）．
（2）当销售单价为多少元时，公司每日能够获得最大利润？最大利润是多少？
（3）根据物价局规定，这种纪念品的销售单价不得高于32元，如果公司要获得每日不低于350元的利润，那么制造这种纪念花灯每日的最低制造成本需要多少元？
