Question

【题目】已知：在Rt△ABC中，∠BAC=90°，AB=AC，点D为BC边中点．点M为线段BC上的一个动点（不与点C，点D重合），连接AM，将线段AM绕点M顺时针旋转90°，得到线段ME，连接EC．

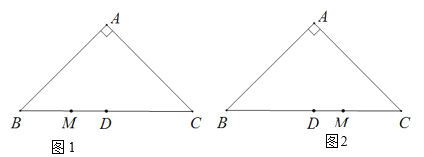
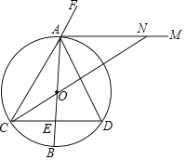
（1）如图1，若点M在线段BD上．

① 依据题意补全图1；

② 求∠MCE的度数．

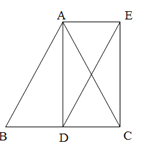
（2）如图2，若点M在线段CD上，请你补全图形后，直接用等式表示线段AC、CE、CM之间的数量关系 ．

Answer 1

【答案】（1）①见解析；②∠MCE=∠F=45°；（2）

【解析】

（1） ① 依据题意补全图即可；② 过点M作BC边的垂线交CA延长线于点F ，利用同角的余角相等，得到∠FMA= ∠CME，再通过等腰三角形的判定得到FM=MC，再通过判断，得到∠MCE的度数.

（2）通过证明，得到 AF=EC，将转化为，再在Rt△FMC中，利用边角关系求出FC=，即可得到.

（1） ① 补全图1：

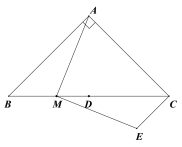
② 解：过点M作BC边的垂线交CA延长线于点F

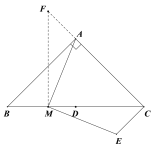
∵FM⊥BC

∴ ∠FMC =90°

∴ ∠FMA+∠AMC=90°

∵将线段AM绕点M顺时针旋转90°，得到线段ME

∴∠AME=90° ，AM=ME

∴ ∠CME+∠AMC=90°

∴∠FMA= ∠CME

∵∠BAC=90°，AB=AC，

∴∠FCM=45°

∴∠F=∠FCM=45°

∴FM=MC

在△FMA和△CME中

∴

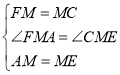
∴ ∠MCE=∠F=45°

（2）解：过点M作BC边的垂线交CA延长线于点F

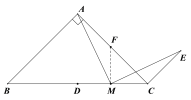
∵FM⊥BC

∴ ∠FMC =90°

∴ ∠FME+∠EMC=90°

∵将线段AM绕点M顺时针旋转90°，得到线段ME

∴∠AME=90° ，AM=ME

∴∠FME +∠AMF=90°

∴∠EMC = ∠AMF

∵∠BAC=90°，AB=AC，

∴∠FCM=45°

∴∠MFC=90°-∠FCM=45°

∴FM=MC

在△FMA和△CME中

∴

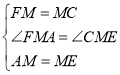
∴ AF=EC

∴

∵∠FCM=45°，∠FMC=90°

∴FC=

∴

综上所述，