��Ŀ����
����Ŀ��֪ʶǨ��
��![]() ��
��![]() ʱ����Ϊ
ʱ����Ϊ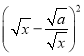 ��
��![]() ,����
,����![]() ��
��![]() ,�Ӷ�
,�Ӷ�![]() ��
��![]() (��
(��![]() ʱȡ�Ⱥ�).
ʱȡ�Ⱥ�).
�Ǻ���![]() ,���������ۿ�֪����
,���������ۿ�֪����![]() ʱ,�ú�������СֵΪ
ʱ,�ú�������СֵΪ![]()
ֱ��Ӧ��
��֪����![]() �뺯��
�뺯��![]() , ��
, ��![]() ____ʱ,
____ʱ,![]() ȡ����СֵΪ___.
ȡ����СֵΪ___.
����Ӧ��
��֪����![]() �뺯��
�뺯��![]() ,��
,��![]() ����Сֵ,��ָ��ȡ�ø���Сֵʱ��Ӧ��
����Сֵ,��ָ��ȡ�ø���Сֵʱ��Ӧ��![]() ��ֵ.
��ֵ.
ʵ��Ӧ��
��֪ij������һ������ɱ����������������֣�һ�ǹ̶�����,��![]() Ԫ������ȼ�ͷ�,ÿǧ��Ϊ
Ԫ������ȼ�ͷ�,ÿǧ��Ϊ![]() Ԫ�������۾ɷ�,����·�̵�ƽ��������,����ϵ��Ϊ
Ԫ�������۾ɷ�,����·�̵�ƽ��������,����ϵ��Ϊ![]() .�������һ�������·��Ϊ
.�������һ�������·��Ϊ![]() ǧ��,��
ǧ��,��![]() Ϊ����ʱ,������ƽ��ÿǧ������ɱ���ͣ�����Ƕ���Ԫ��
Ϊ����ʱ,������ƽ��ÿǧ������ɱ���ͣ�����Ƕ���Ԫ��
���𰸡�ֱ��Ӧ�� 1, 2������Ӧ���� ![]() ����СֵΪ
����СֵΪ![]() ,
,![]() ʱȡ�ø���Сֵ��ʵ��Ӧ��2.8
ʱȡ�ø���Сֵ��ʵ��Ӧ��2.8
��������
ֱ�����ã�����ֱ���������������Ľ��ۣ����ɵó������
�������ã��ȵó�![]() �ı���ʽ��Ȼ��x+1������һ�����壬�̶��������������ۼ��ɣ�
�ı���ʽ��Ȼ��x+1������һ�����壬�̶��������������ۼ��ɣ�
ʵ�����ã�����ʻxǧ�ķ���Ϊy����ɱ�ʾ��ƽ��ÿǧ������ɱ������������Ľ��ۼ��ɵó��𰸣�
ֱ��Ӧ�� 1, 2
����Ӧ�� ��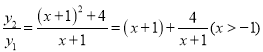
��![]() ����СֵΪ
����СֵΪ![]() ,
,
��![]() ,��
,��![]() ʱȡ�ø���Сֵ
ʱȡ�ø���Сֵ
ʵ��Ӧ��
�⣺�������ƽ��ÿǧ������ɱ�Ϊ![]() Ԫ,��
Ԫ,��![]()
![]() ,
,
�൱![]() (ǧ��)ʱ, ������ƽ��ÿǧ������ɱ�
(ǧ��)ʱ, ������ƽ��ÿǧ������ɱ�![]() ���
���
��ͳɱ�Ϊ![]() Ԫ.
Ԫ.

��ϰ��ϵ�д�
 �·Ƿ��̸����100��ϵ�д�
�·Ƿ��̸����100��ϵ�д�
�����Ŀ