[题目]已知关于的方程(1)无论取任何实数.方程总有实数根吗?试做出判断并证明你的结论.(2)抛物线的图象与轴两个交点的横坐标均为整数.且也为正整数.若.是此抛物线上的两点.且.请结合函数图象确定实数的取值范围. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知关于的方程

（1）无论取任何实数，方程总有实数根吗？试做出判断并证明你的结论.

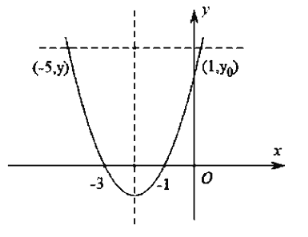
（2）抛物线的图象与轴两个交点的横坐标均为整数，且也为正整数.若，是此抛物线上的两点，且，请结合函数图象确定实数的取值范围.

【答案】（1）无论取任何实数，方程总有实数根；证明见解析；（2）.

【解析】

（1）由题意分当时以及当时，利用根的判别式进行分析即可；

（2）根据题意令，代入抛物线解析式，并利用二次函数图像性质确定实数的取值范围.

解：（1）①当时，方程为时，，所以方程有实数根；

②当时，

所以方程有实数根

综上所述，无论取任何实数，方程总有实数根.

（2）令，则，解方程，

∵二次函数图象与轴两个交点的横坐标均为整数，且为正整数

∴

∴该抛物线解析式

∴对称轴

∵，是抛物钱上的两点，且

∴

练习册系列答案

相关题目

【题目】随机抽取某小吃店一周的营业额(单位: 元)如下表:

星期一	星期二	星期三	星期四	星期五	星期六	星期日	合计

（1）分析数据，填空:这组数据的平均数是元，中位数是元，众数是元.

（2）估计一个月(按天计算)的营业额,星期一到星期五营业额相差不大，用这天的平均数估算合适么?简要说明理由.

【题目】一蓄水池每小时的排水量V（m3/h）与排完水池中的水所用的时间t（h）之间成反比例函数关系，其图象如图所示．

（1）求V与t之间的函数表达式；

（2）若要2h排完水池中的水，那么每小时的排水量应该是多少？

（3）如果每小时排水量不超过4000m3，那么水池中的水至少要多少小时才能排完？

【题目】在每个小正方形的边长为1的网格图形中，每个小正方形的顶点称为格点．以顶点都是格点的正方形ABCD的边为斜边，向内作四个全等的直角三角形，使四个直角顶点E，F，G，H都是格点，且四边形EFGH为正方形，我们把这样的图形称为格点弦图．例如，在如图1所示的格点弦图中，正方形ABCD的边长为，此时正方形EFGH的而积为5．问：当格点弦图中的正方形ABCD的边长为时，正方形EFGH的面积的所有可能值是_____（不包括5）．