题目内容
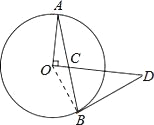
【题目】如图,AB是圆O的弦,OA⊥OD,AB,OD相交于点C,且CD=BD.
(1)判断BD与圆O的位置关系,并证明你的结论;
(2)当OA=3,OC=1时,求线段BD的长.

【答案】(1)见解析;(2)4
【解析】试题分析: (1)连接OB,由BD=CD,利用等边对等角得到∠DCB=∠DBC,再由AO垂直于OD,得到三角形AOC为直角三角形,得到两锐角互余,等量代换得到OB垂直于BD,即可得证;
(2)设BD=x,则OD=x+1,在RT△OBD中,根据勾股定理得出32+x2=(x+1)2,通过解方程即可求得.
试题解析:
(1)证明:连接OB,
∵OA=OB,DC=DB,
∴∠A=∠ABO,∠DCB=∠DBC,
∵AO⊥OD,
∴∠AOC=90°,即∠A+∠ACO=90°,
∵∠ACO=∠DCB=∠DBC,
∴∠ABO+∠DBC=90°,即OB⊥BD,
则BD为圆O的切线;
(2)解:设BD=x,则OD=x+1,而OB=OA=3,
在RT△OBD中,OB2+BD2=OD2,
即32+x2=(x+1)2,
解得x=4,
∴线段BD的长是4.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目







