Question

【题目】如图，在平面直角坐标系中，矩形AOBC的边AO在x轴的负半轴上，边OB在y轴的负半轴上．且AO＝12，OB＝9．抛物线y＝﹣x2+bx+c经过点A和点B．

（1）求抛物线的表达式；

（2）在第二象限的抛物线上找一点M，连接AM，BM，AB，当△ABM面积最大时，求点M的坐标；

（3）点D是线段AO上的动点，点E是线段BO上的动点，点F是射线AC上的动点，连接EF，DF，DE，BD，且EF是线段BD的垂直平分线．当CF＝1时．

①直接写出点D的坐标　 　；

②若△DEF的面积为30，当抛物线y＝﹣x2+bx+c经过平移同时过点D和点E时，请直接写出此时的抛物线的表达式　 　．

Answer 1

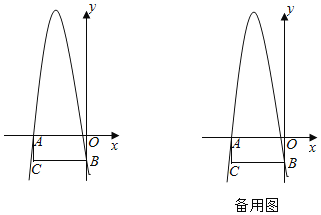
【答案】（1）y＝﹣x2﹣x﹣9；（2）M(﹣6，31.5)；（3）①(﹣12+3，0)或(﹣3，0)，②y＝﹣x2﹣x﹣4

【解析】

（1）利用待定系数法把问题转化为解方程组即可解决问题．

（2）如图1中，设M（m，﹣m2﹣m﹣9），根据S△ABM＝S△ACM+S△MBC﹣S△ACB构建二次函数，利用二次函数的性质解决问题即可．

（3）①分两种情形：如图2中，当点F在AC的延长线设时，连接DF，FB．设D（m，0）．根据FD＝FB，构建方程求解．当点F在线段AC上时，同法可得．

②根据三角形的面积求出D，E的坐标，再利用待定系数法解决问题即可．

解：（1）由题意A（﹣12，0），B（0，﹣9），

把A，B的坐标代入y＝﹣x2+bx+c，

得到，

解得：，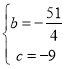

∴抛物线的解析式为y＝﹣x2﹣x﹣9．

（2）如图1中，设M（m，﹣m2﹣m﹣9），

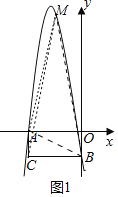
S△ABM＝S△ACM+S△MBC﹣S△ACB

＝×9×（m+12）+×12×（﹣m2﹣m﹣9+9）﹣×12×9

＝﹣6m2﹣72m

＝﹣6（m+6）2+216，

∵﹣6＜0，

∴m＝﹣6时，△ABM的面积最大，此时M（﹣6，31.5）．

（3）①如图2中，当点F在AC的延长线设时，连接DF，FB．设D（m，0）．

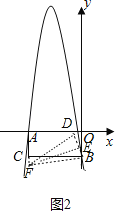
∵EF垂直平分线段BD，

∴FD＝FB，

∵F（﹣12，﹣10），B（0，﹣9），

∴102+（m+12）2＝122+12，

∴m＝﹣12﹣3（舍弃）或﹣12+3，

∴D（﹣12+3，0）．

当点F在线段AC上时，同法可得D（﹣3，0），

综上所述，满足条件的点D的坐标为（﹣12+3，0）或（﹣3，0）．

故答案为（﹣12+3，0）或（﹣3，0）．

②由①可知∵△EF的面积为30，

∴D（﹣3，0），E（0，﹣4），

把D，E代入y＝﹣x2+b′x+c′，

可得，

解得：，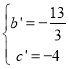

∴抛物线的解析式为y＝﹣x2﹣x﹣4．

故答案为：y＝﹣x2﹣x﹣4．