题目内容
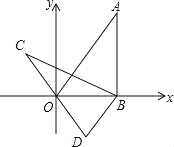
【题目】已知二次函数y=ax2+bx+6的图像开口向下,与x轴交于点A(-6,0)和点B(2,0),与y轴交于点C,点P是该函数图像上的一个动点(不与点C重合)

(1) 求二次函数的关系式;
(2)如图1当点P是该函数图像上一个动点且在线段![]() 的上方,若△PCA的面积为12,求点P的坐标;
的上方,若△PCA的面积为12,求点P的坐标;
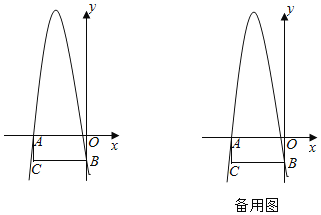
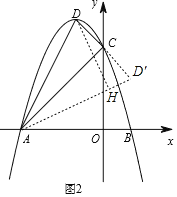
(3)如图2,该函数图像的顶点为D,在该函数图像上是否存在点E,使得∠EAB=2∠DAC,若存在请直接写出点E的坐标;若不存在请说明理由.
【答案】(1) ![]() ;(2)(﹣2,8)或(﹣4,6);(3)
;(2)(﹣2,8)或(﹣4,6);(3) ![]()
![]() 或
或![]() .
.
【解析】
(1)由题意设函数的表达式为:![]() 结合已知函数解析式即可求解;
结合已知函数解析式即可求解;
(2)由点P在线段![]() 的上方,设
的上方,设![]() 连接
连接![]()
![]() ,从而可得答案;
,从而可得答案;
(3)证明![]() 为直角三角形,延长DC至D′使CD=CD′,连接AD′,过点D作DH⊥AD′,计算sin∠DAC ,sin2∠DAC=sin∠DAD′得到sin∠EAB,tan∠EAB ,利用一次函数的性质得一次函数是解析式,联立解析式解方程组即可求解.
为直角三角形,延长DC至D′使CD=CD′,连接AD′,过点D作DH⊥AD′,计算sin∠DAC ,sin2∠DAC=sin∠DAD′得到sin∠EAB,tan∠EAB ,利用一次函数的性质得一次函数是解析式,联立解析式解方程组即可求解.
解:(1)![]() 抛物线与x轴交于点A(-6,0)和点B(2,0),
抛物线与x轴交于点A(-6,0)和点B(2,0),
![]() 设函数的表达式为:
设函数的表达式为:![]()
![]() 二次函数
二次函数![]()
![]()
解得:![]()
![]() 函数的表达式为:
函数的表达式为:![]() .
.
(2)如图1所示,![]() 在
在![]() 的上方,
的上方,
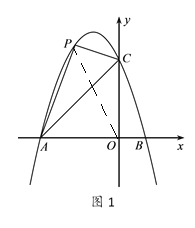
连接![]()
![]()
设![]()
把![]() 代入
代入![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
解得:![]()
所以点P坐标为![]() 或
或![]()
(3)![]() 抛物线为:
抛物线为:![]() ,
,![]() 为顶点,
为顶点,
![]()
![]()
![]()
则![]()
![]()
![]()
![]()
![]()
延长DC至D′使CD=CD′,连接AD′,
过点D作DH⊥AD′, 则![]()
![]()
即:![]()
解得:![]()

![]() ∠EAB=2∠DAC,
∠EAB=2∠DAC,
![]()
①当点E在AB上方时, 则直线AE的表达式为:![]() ,
,
将点![]() 坐标代入上式:
坐标代入上式:![]()
![]()
直线AE的表达式为:![]()

解得: 或
或![]() (舍去)
(舍去)
即点![]()
②当点E在AB下方时,![]()
设直线![]() 为:
为:![]()
将点![]() 坐标代入上式:
坐标代入上式:![]()
![]()
![]() 直线
直线![]() 为:
为:![]()
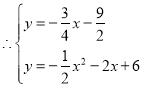
解得: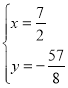 或
或![]() (舍去)
(舍去)
![]()
综上,点![]() 或
或![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目