Question

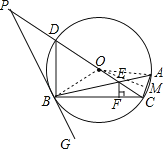
【题目】如图，△ABC内接于⊙O，∠CBG=∠A，CD为直径，OC与AB相交于点E，过点E作EF⊥BC，垂足为F，延长CD交GB的延长线于点P，连接BD．

（1）求证：PG与⊙O相切；

（2）若=，求的值；

（3）在（2）的条件下，若⊙O的半径为8，PD=OD，求OE的长．

Answer 1

【答案】（1）证明见解析；（2）；（3）OE=2﹣4．

【解析】

（1）要证PG与⊙O相切只需证明∠OBG=90°，由∠A与∠BDC是同弧所对圆周角且∠BDC=∠DBO可得∠CBG=∠DBO，结合∠DBO+∠OBC=90°即可得证；

（2）求需将BE与OC或OC相等线段放入两三角形中，通过相似求解可得，作OM⊥AC、连接OA，证△BEF∽△OAM得，由AM=AC、OA=OC知，结合即可得；

（3）Rt△DBC中求得BC=8、∠DCB=30°，在Rt△EFC中设EF=x，知EC=2x、FC=x、BF=8﹣x，继而在Rt△BEF中利用勾股定理求出x的，从而得出答案．

（1）如图，连接OB，则OB=OD，

∴∠BDC=∠DBO，

∵∠BAC=∠BDC、∠BDC=∠GBC，

∴∠GBC=∠BDC，

∵CD是⊙O的切线，

∴∠DBO+∠OBC=90°，

∴∠GBC+∠OBC=90°，

∴∠GBO=90°，

∴PG与⊙O相切；

（2）过点O作OM⊥AC于点M，连接OA，

则∠AOM=∠COM=∠AOC，

∵，

∴∠ABC=∠AOC，

又∵∠EFB=∠OGA=90°，

∴△BEF∽△OAM，

∴，

∵AM=AC，OA=OC，

∴，

又∵，

∴；

（3）∵PD=OD，∠PBO=90°，

∴BD=OD=8，

在Rt△DBC中，BC==8，

又∵OD=OB，

∴△DOB是等边三角形，

∴∠DOB=60°，

∵∠DOB=∠OBC+∠OCB，OB=OC，

∴∠OCB=30°，

∴，=，

∴可设EF=x，则EC=2x、FC=x，

∴BF=8﹣x，

在Rt△BEF中，BE2=EF2+BF2，

∴100=x2+（8﹣x）2，

解得：x=6±，

∵6+＞8，舍去，

∴x=6﹣，

∴EC=12﹣2，

∴OE=8﹣（12﹣2）=2﹣4．