题目内容
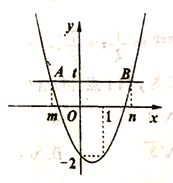
【题目】如图,在![]() 中,点
中,点![]() ,点
,点![]() 在
在![]() 轴正半轴上,以
轴正半轴上,以![]() 为一边作等腰直角
为一边作等腰直角![]() ,使得点
,使得点![]() 在第一象限.
在第一象限.

(1)求出所有符合题意的点![]() 的坐标;
的坐标;
(2)在![]() 内部存在一点
内部存在一点![]() ,使得
,使得![]() 之和最小,请求出这个和的最小值.
之和最小,请求出这个和的最小值.
【答案】(1)![]() ,
,![]() ,
,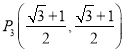 ;(2)这个和的最小值
;(2)这个和的最小值![]() .
.
【解析】
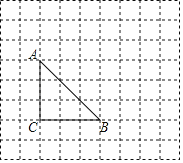
(1)根据C(1,0),得到OC=1,解直角三角形得到AC=2,OA=![]() ,如图1,①当AC=AP,∠CAP=90°,过P1作P1B⊥y轴于B,②当AC=CP,∠ACP=90°,过P2作P2D⊥x轴于D,③当CP=AP,∠APC=90°,过P3作P3E⊥x轴于E,解直角三角形即可得到结论;
,如图1,①当AC=AP,∠CAP=90°,过P1作P1B⊥y轴于B,②当AC=CP,∠ACP=90°,过P2作P2D⊥x轴于D,③当CP=AP,∠APC=90°,过P3作P3E⊥x轴于E,解直角三角形即可得到结论;
(2)任取△AOC内一点Q,连接AQ、BQ、CQ,将△ACQ绕点C顺时针旋转60°得到△A′CQ′,于是得到当A′Q′,OQ,QQ′这三条线段在同一直线时最短,即AQ+OQ+CQ的最小值=OA′,过A′作A′B⊥x轴于B,解直角三角形即可得到结论.
(1)如图1,
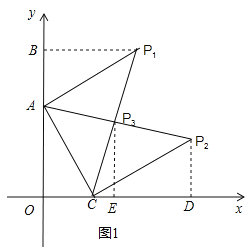
∵C(1,0),
∴OC=1,
∵在Rt△AOC中,∠A=30°,
∴AC=2,OA=![]() ,
,
如图1,①当AC=AP,∠CAP=90°,过P1作P1B⊥y轴于B,
则△ABP1≌△COA,
∴AB=OC=1,BP1=AO=![]() ,
,
∴OB=1+![]() ,
,
∴P1(![]() ,1+
,1+![]() );
);
②当AC=CP,∠ACP=90°,过P2作P2D⊥x轴于D,
同理可得:CD=OA=![]() ,P2D=1,
,P2D=1,
∴P2(1+![]() ,1);
,1);
③当CP=AP,∠APC=90°,过P3作P3E⊥x轴于E,
则P3是AP2的中点,
∴OE=![]() OD=
OD=![]() ,P3E=
,P3E=![]() (OA+P2D)=
(OA+P2D)=![]() ,
,
∴P3(![]() ,
,![]() );
);
综上所述,P(![]() ,1+
,1+![]() ),(1+
),(1+![]() ,1),(
,1),(![]() ,
,![]() );
);
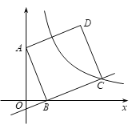
(2)如图2,任取△AOC内一点Q,连接AQ、OQ、CQ,
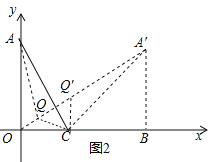
将△ACQ绕点C顺时针旋转60°得到△A′CQ′,
∴A′C=AC=2,CQ=CQ′,AQ=A′Q′,∠ACA′=∠QCQ′=60°,
∴△QCQ′是等边三角形,
∴CQ=QQ′,
∴AQ+OQ+CQ=A′Q′+OQ+QQ′,
∴当A′Q′,OQ,QQ′这三条线段在同一直线时最短,即AQ+OQ+CQ的最小值=OA′,
∵∠ACO=∠ACA′=60°,
∴∠A′CB=60°,
过A′作A′B⊥x轴于B,
∴BC=![]() A′C=1,A′B=
A′C=1,A′B=![]() ,
,
∴OB=2,
∴![]() ,
,
∴AQ、OQ、CQ之和的最小值是![]() .
.

 阅读快车系列答案
阅读快车系列答案