题目内容
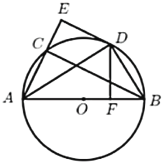
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 是
是![]() 上一点,
上一点,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() .若
.若![]() ,
,![]() ,求
,求![]() 的长度.
的长度.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OD,由等腰三角形的性质及角平分线的性质得出∠ADO=∠DAE,从而OD∥AE,由DE∥BC得∠E=90°,由两直线平行,同旁内角互补得出∠ODE=90°,由切线的判定定理得出答案;
(2)先由直径所对的圆周角是直角得出∠ADB=90°,再由OF=1,BF=2得出OB的值,进而得出AF和BA的值,然后证明△DBF∽△ABD,由相似三角形的性质得比例式,从而求得BD2的值,求算术平方根即可得出BD的值.
解:(1)连接OD,如图:
∵OA=OD,
∴∠OAD=∠ADO,
∵AD平分∠CAB,
∴∠DAE=∠OAD,
∴∠ADO=∠DAE,
∴OD∥AE,
∵DE∥BC,
∴∠E=90°,
∴∠ODE=180°∠E=90°,
∴DE是⊙O的切线;
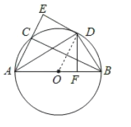
(2)因![]() 为直径,则
为直径,则![]()
∵![]() ,
,![]()
∴OB=3
∴![]() ,
,![]()
∵∠ADB=∠DFB=90°, ∠B=∠B
∴△DBF∽△ABD
∴![]()
∴![]()
所以![]() .
.

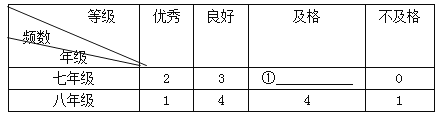
【题目】《中学生体质健康标准》规定的等级标准为:90分及以上为优秀,80~89分为良好,60~79分为及格,59分及以下为不及格.某校为了解七、八年级学生的体质健康情况,现从两年级中各随机抽取10名同学进行体质健康检测,并对成绩进行分析.成绩如下:
七年级 | 80 | 74 | 83 | 63 | 90 | 91 | 74 | 61 | 82 | 62 |
八年级 | 74 | 61 | 83 | 91 | 60 | 85 | 46 | 84 | 74 | 82 |
(1)根据上述数据,补充完成下列表格中序号.
整理数据:
分析数据:
年级 | 平均数 | 众数 | 中位数 |
七年级 | ②_________ | 74 | 77 |
八年级 | 74 | 74 | ③____________ |
(2)该校目前七年级有300人,八年级有200人,试估计两个年级体质健康等级达到优秀的学生共有多少人?
(3)结合上述数据信息,你认为哪个年级学生的体质健康情况更好,并说明理由.