ЬтФПФкШн
ЁОЬтФПЁПМзЁЂввСНГЕбиЭЌвЛЬѕЕРТЗДг![]() ЕиГіЗЂЯђ1200
ЕиГіЗЂЯђ1200![]() ЭтЕФ
ЭтЕФ![]() ЕиЪфЫЭНєМБЮязЪЃЌМздкЭОжаанЯЂСЫ3аЁЪБЃЌанЯЂЧАКѓЕФЫйЖШВЛЭЌЃЌзюКѓСНГЕЭЌЪБЕНДя
ЕиЪфЫЭНєМБЮязЪЃЌМздкЭОжаанЯЂСЫ3аЁЪБЃЌанЯЂЧАКѓЕФЫйЖШВЛЭЌЃЌзюКѓСНГЕЭЌЪБЕНДя![]() ЕиЃЌШчЭММзЁЂввСНГЕЕН
ЕиЃЌШчЭММзЁЂввСНГЕЕН![]() ЕиЕФОрРы
ЕиЕФОрРы![]() ЃЈЧЇУзЃЉгыввГЕааЪЛЪБМф
ЃЈЧЇУзЃЉгыввГЕааЪЛЪБМф![]() ЃЈаЁЪБЃЉжЎМфЕФКЏЪ§ЭМЯѓЃЎ
ЃЈаЁЪБЃЉжЎМфЕФКЏЪ§ЭМЯѓЃЎ
ЃЈ1ЃЉМзГЕанЯЂЧАЕФааЪЛЫйЖШЮЊ ЧЇУз/ЪБЃЌввГЕЕФЫйЖШЮЊ ЧЇУз/ЪБЃЛ
ЃЈ2ЃЉЕБ9Ём![]() Ём15ЃЌЧѓМзГЕЕФааЪЛТЗГЬ
Ём15ЃЌЧѓМзГЕЕФааЪЛТЗГЬ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉжБНгаДГіМзГіЗЂЖрГЄЪБМфгыввдкЭОжаЯргіЃЎ
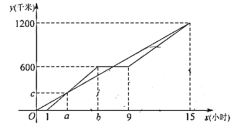
ЁОД№АИЁПЃЈ1ЃЉ120ЃЌ80ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ2аЁЪБЃЌ6.5аЁЪБ
ЃЛЃЈ3ЃЉ2аЁЪБЃЌ6.5аЁЪБ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнМздкЭОжаанЯЂСЫ3аЁЪБЃЌНсКЯКЏЪ§ЭМЯѓПЩЧѓГіbЕФжЕЃЌНјЖјгЩТЗГЬЁТЪБМф=ЫйЖШЃЌБуПЩЧѓЕУНсЙћЃЛ
ЃЈ2ЃЉгУД§ЖЈЯЕЪ§ЗЈНјааНтД№БуПЩЃЛ
ЃЈ3ЃЉЩшМзГіЗЂ![]() аЁЪБгыввдкЭОжаЯргіЃЌЗжСНжжЧщПіЃКдкМзжаЭОанЯЂЧАЯргіЃЌМзжаЭОанЯЂЪБЯргіЃЎЗжБ№СаГівЛдЊвЛДЮЗНГЬНтД№ЃЎ
аЁЪБгыввдкЭОжаЯргіЃЌЗжСНжжЧщПіЃКдкМзжаЭОанЯЂЧАЯргіЃЌМзжаЭОанЯЂЪБЯргіЃЎЗжБ№СаГівЛдЊвЛДЮЗНГЬНтД№ЃЎ
ИљОнЭМаЮПЩЕУЃК
ввГЕДгГіЗЂЕНжеЕуЙВгУЪБ15аЁЪБТЗГЬ1200ЧЇУзЃЌЫљвдввГЕЕФЫйЖШ=1200ЁТ15=80ЧЇУз/ЪБЃЛ
МзГЕЙВгУЪБ14аЁЪБЃЌанЯЂ3аЁЪБЃЌанЯЂКѓааЪЛ6аЁЪБЃЌЫљвданЯЂЧАааЪЛ5аЁЪБЃЌанЯЂЧАааЪЛТЗГЬ600ЧЇУзЃЌМзГЕанЯЂЧАЕФааЪЛЫйЖШ=600ЁТ5=120ЧЇУз/ЪБЃЛ
ЙЪД№АИЮЊЃК120ЃЌ80ЃЎ
ЃЈ2ЃЉЩшЕБ![]() ЪБЃЌМзГЕааЪЛТЗГЬ
ЪБЃЌМзГЕааЪЛТЗГЬ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЮЊ
ЕФКЏЪ§ЙиЯЕЪНЮЊ![]() ЃЎ
ЃЎ
АбЕу![]() ЁЂ
ЁЂ![]() ДњШыПЩЕУЃК
ДњШыПЩЕУЃК
![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЎ
ЃЎ
ЕБ![]() ЪБЃЌМзГЕааЪЛТЗГЬ
ЪБЃЌМзГЕааЪЛТЗГЬ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЮЊ
ЕФКЏЪ§ЙиЯЕЪНЮЊ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉЩшМзГіЗЂxаЁЪБгыввдкЭОжаЯргіЃЌИљОнЬтвтЕУЃЌ
ЂйдкМзЭОжаанЯЂЧАЯргіЃЌга120x-80x=80ЁС1ЃЌ
НтЕУЃЌx=2ЃЛ
ЂкдкМзЭОжаанЯЂЪБЯргіЃЌга80ЃЈx+1ЃЉ=600ЃЌ
НтЕУЃЌx=6.5ЃЌ
злЩЯЃЌМзГіЗЂ2аЁЪБЛђ6.5аЁЪБгыввдкЭОжаЯргіЃЎЃЎ