题目内容
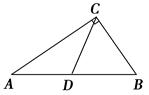
在钝角三角形ABC中，AB＝AC，点D是BC上一点，AD把△ABC分成两个等腰三角形，则∠BAC的度数为( )．
| A．150° | B．124° |
| C．120° | D．108° |
D
根据题意，△ABD、△ADC是等腰三角形，∠B＝∠BAD，∠ADC＝∠DAC，
而AB＝AC，∠B＝∠C，根据三角形外角的性质，
∠ADC＝∠B＋∠BAD＝2∠B，
设∠B＝x°，则∠DAC＝∠ADC＝2x°，∠BAC＝3x°，
根据三角形内角和，x＋x＋3x＝180，解得x＝36，所以∠BAC＝3x°＝108°.
而AB＝AC，∠B＝∠C，根据三角形外角的性质，
∠ADC＝∠B＋∠BAD＝2∠B，
设∠B＝x°，则∠DAC＝∠ADC＝2x°，∠BAC＝3x°，
根据三角形内角和，x＋x＋3x＝180，解得x＝36，所以∠BAC＝3x°＝108°.
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
