Question

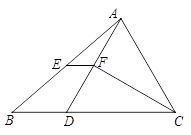
三角形ABC中，∠A=60°，则内角∠B，∠C的角平分线相交所成的角为           。

Answer 1

120°和60°

试题分析：因为三角形的内角和是180度，所以∠B+∠C=180°-∠A=180°-60°=120°，又因为∠DFE=∠BFC，∠BFC=180°-（∠FBC+∠FCB），因为角平分线CD、EF相交于F，所以∠FBC+∠FCB=（∠B+∠C）÷2=120°÷2=60°，再代入∠DFE=∠BFC=180°-（∠FBC+∠FCB），即可解答．
试题解析：∠B+∠C=180°-∠A=180°-60°=120°，
又因为∠DFE=∠BFC，∠BFC=180°-（∠FBC+∠FCB），
因为角平分线CD、EF相交于F，
所以∠FBC+∠FCB=（∠B+∠C）÷2=120°÷2=60°，
∠DFE=180°-（∠FBC+∠FCB），
=180°-60°，
=120°；
∠DFE的邻补角的度数为：180°-120°=60°．