题目内容
如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE.已知∠BAC＝30°，EF⊥AB，垂足为F，连结DF.
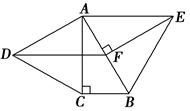
(1)试证明AC＝EF.
(2)求证：四边形ADFE是平行四边形．
(1)试证明AC＝EF.
(2)求证：四边形ADFE是平行四边形．
见解析
证明：(1)∵等边△ABE中，EF⊥AB
∴EF平分∠AEB，∴∠AEF＝
∠AEB＝30°∵∠BAC＝30°，∴∠AEF＝∠BAC
又∵∠AFE＝∠ACB＝90°，AE＝AB
∴△ABC≌△EAF ∴AC＝EF
(2)∵等边△ACD中，∠DAC＝60°
而∠CAB＝30°，∴∠DAF＝90°＝∠AFE
∴AD∥EF 又∵AD＝AC，AC＝EF
∴AD＝EF.∴四边形ADFE是平行四边形．
练习册系列答案
名校课堂系列答案
相关题目
