Question

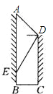
【题目】已知AD为⊙O的直径，BC为⊙O的切线，切点为M，分别过A，D两点作BC的垂线，垂足分别为B，C，AD的延长线与BC相交于点E．

（1）求证：△ABM∽△MCD；

（2）若AD=8，AB=5，求ME的长．

Answer 1

【答案】（1）证明见解析（2）4

【解析】

（1）由AD为直径，得到所对的圆周角为直角，利用等角的余角相等得到一对角相等，进而利用两对角对应相等的三角形相似即可得证；

（2）连接OM，由BC为圆的切线，得到OM与BC垂直，利用锐角三角函数定义及勾股定理即可求出所求．

（1）∵AD为圆O的直径，∴∠AMD=90°．

∵∠BMC=180°，∴∠2+∠3=90°．

∵∠ABM=∠MCD=90°，∴∠2+∠1=90°，∴∠1=∠3，∴△ABM∽△MCD；

（2）连接OM．

∵BC为圆O的切线，∴OM⊥BC．

∵AB⊥BC，∴sin∠E==，即=．

∵AD=8，AB=5，∴=，即OE=16，根据勾股定理得：ME===4．