题目内容

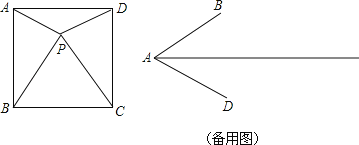
【题目】如图，矩形矩形，连结，延长分别交、于点、，延长、交于点，一定能求出面积的条件是（ ）

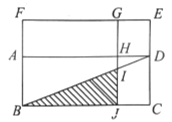
A.矩形和矩形的面积之差B.矩形和矩形的面积之差

C.矩形和矩形的面积之差D.矩形和矩形的面积之差

【答案】B

【解析】

根据相似多边形的性质得到，即AF·BC=AB·AH①．然后根据IJ∥CD可得，，再结合以及矩形中的边相等可以得出IJ=AF=DE．最后根据S△BIJ=BJ·IJ=BJ·DE=(BC-DH)·DE=BC·AF-DH·DE②，结合①②可得出结论．

解：∵矩形ABCD∽矩形FAHG，

，∴AF·BC=AB·AH，

又IJ∥CD，∴，

又DC=AB，BJ=AH，∴，∴IJ=AF=DE．

S△BIJ=BJ·IJ=BJ·DE=(BC-DH)·DE=BC·AF-DH·DE=AB·AH-DH·DE=(S矩形ABJH -S矩形HDEG)．

∴能求出△BIJ面积的条件是知道矩形ABJH和矩形HDEG的面积之差．

故选：B．

练习册系列答案
相关题目

【题目】如图，抛物线与轴交于、两点，与轴交于点,抛物线的对称轴为直线，交抛物线于点,交轴于点．

　　　　　　　　

（1）求抛物线的函数表达式及点、点的坐标；

（2）抛物线对称轴上的一动点从点出发，以每秒1个单位的速度向上运动，连接，，设运动时间为秒（），在点的运动过程中，请求出：当为何值时，？

（3）若点在抛物线上、两点之间运动（点不与点、重合），在运动过程中，设点的横坐标为，的面积为，求关于的函数关系式，并求为何值时有最大值，最大值是多少？

【题目】定义：点P是四边形ABCD内一点，若三角形△PAB，△PBC，△PCD，△PDA均为等腰三角形，则称点P是四边形ABCD的一个“准中心”，如，正方形的中心就是它的一个“准中心”．

（1）如图，已知点P是正方形ABCD内的一点，且∠PBC＝∠PCB＝60°，证明点P是正四边形ABCD的一个“准中心”；

（2）填空：正方形ABCD共有　 　个“准中心”；

（3）已知∠BAD＝60°，AB＝AD＝6，点C是∠BAD平分线上的动点，问在四边形ABCD的对角线AC上最多存在几个“准中心”点P（自行画出示意图），并求出每个“准中心”点P对应线段AC的长（精确到个位）．

【题目】如图，AD是⊙O的直径，AB为⊙O的弦，OP⊥AD，OP与AB的延长线交于点P，点C在OP上，满足∠CBP＝∠ADB．

（1）求证：BC是⊙O的切线；

（2）若OA＝2，AB＝1，求线段BP的长．

【题目】如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．

（1）求证：AF=DC；

（2）若AB⊥AC，试判断四边形ADCF的形状，并证明你的结论．

【题目】在一个不透明的小布袋中装有4个质地、大小完全相同的小球，它们分别标有数字0，1，2，3，小明从布袋里随机摸出一个小球，记下数字为，小红在剩下的3个小球中随机摸出一个小球，记下数字为，这样确定了点的坐标．

（1）画树状图或列表，写出点所有可能的坐标；

（2）小明和小红约定做一个游戏，其规则为：若在第一象限，则小明胜；否则，小红胜；这个游戏公平吗？请你作出判断并说明理由．

【题目】如图，在Rt△ABC中，∠BAC=90°，AB=1，tanC=，以点A为圆心，AB长为半径作弧交AC于D，分别以B、D为圆心，以大于BD长为半径作弧，两弧交于点E，射线AE与BC于F，过点F作FG⊥AC于G，则FG的长为______．

【题目】如图，将抛物线M1：y＝ax2+4x向右平移3个单位，再向上平移3个单位，得到抛物线M2，直线y＝x与M1的一个交点记为A，与M2的一个交点记为B，点A的横坐标是﹣3．

（1）求a的值及M2的表达式；

（2）点C是线段AB上的一个动点，过点C作x轴的垂线，垂足为D，在CD的右侧作正方形CDEF．

①当点C的横坐标为2时，直线y＝x+n恰好经过正方形CDEF的顶点F，求此时n的值；

②在点C的运动过程中，若直线y＝x+n与正方形CDEF始终没有公共点，求n的取值范围（直接写出结果）．

【题目】如图，△ABC中，BC＝4，⊙P与△ABC的边或边的延长线相切．若⊙P半径为2，△ABC的面积为5，则△ABC的周长为( )

A.8B.10C.13D.14

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网