题目内容
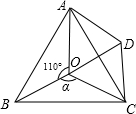
如图，等边△ABC中，D、E分别在AB、AC上，且AD=CE，BE、CD交于点P，若∠ABE：∠CBE=1：2，则∠BDP=______度．
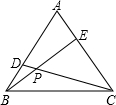
∵等边△ABC
∴∠A=∠ABC=∠ACB=60°，AC=BC
∵∠ABE：∠CBE=1：2
∴∠CBE=
∠ABC=40°
又∵AD=CE
∴△ADC≌△CEB（SAS）
∴∠ACD=∠CBE=40°
∴∠BDP=∠BDC=∠A+∠ACD=60°+40°=100°．
故答案为100°．
∴∠A=∠ABC=∠ACB=60°，AC=BC
∵∠ABE：∠CBE=1：2
∴∠CBE=
| 2 |
| 3 |
又∵AD=CE
∴△ADC≌△CEB（SAS）
∴∠ACD=∠CBE=40°
∴∠BDP=∠BDC=∠A+∠ACD=60°+40°=100°．
故答案为100°．
练习册系列答案
相关题目
