题目内容
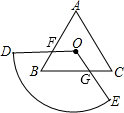
已知等边三角形△ABC和点P,过点P作三边AB、AC、BC的平行线分别交AC、BC、AB于F、G、E,如图①,点P在BC边上可得PE+PF+PG=BC.当点P在△ABC内部时(如图②),点P在△ABC外部时如图③,这两种情况下是否还存在PE+PF+PG=BC的结论?若成立请给予证明,若不成立,那么PE、PF、PG与BC又有怎样的关系,请写出你的猜想,不需证明.
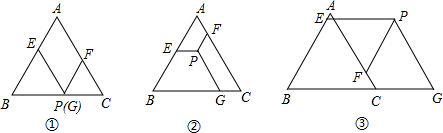

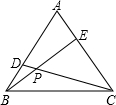
(1)如图②,延长FP,与BC交于点D,
∵等边三角形△ABC,
∴∠A=∠B=∠C=60°
∵PE∥BC,PG∥AC,PF∥AB,
∴∠A=∠B=∠C=∠PGD=∠PDG=∠AEP=∠CFP=60°,EP=BD,
∴△PDG为等边三角形,四边形PECG为等腰梯形,
∴PG=DG,PE=BD,PF=CG,
∵BC=BD+DG+CG,
∴BC=PE+PF+PG,
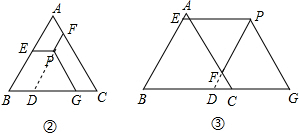
(2)如图③,点P在△ABC外部时,PE+PF+PG=BC的结论不成立,
PE、PF、PG与BC的关系为:PE+PG-PF=BC.
如图③,延长PF,与BC交于点D,
∵等边三角形△ABC,
∴∠A=∠B=∠ACB=60°
∵PE∥BC,PG∥AC,PF∥AB,
∴∠A=∠B=∠ACB=∠PGD=∠PDG=∠AEP=∠CFD=60°,EP=BD,
∴△PDG为等边三角形,四边形PFCG为等腰梯形,
∴PG=DG,PE=BD,PF=CG,
∵BC=BD+DG-CG,
∴BC=PE+PG-PF.
∵等边三角形△ABC,
∴∠A=∠B=∠C=60°
∵PE∥BC,PG∥AC,PF∥AB,
∴∠A=∠B=∠C=∠PGD=∠PDG=∠AEP=∠CFP=60°,EP=BD,
∴△PDG为等边三角形,四边形PECG为等腰梯形,
∴PG=DG,PE=BD,PF=CG,
∵BC=BD+DG+CG,
∴BC=PE+PF+PG,

(2)如图③,点P在△ABC外部时,PE+PF+PG=BC的结论不成立,
PE、PF、PG与BC的关系为:PE+PG-PF=BC.
如图③,延长PF,与BC交于点D,
∵等边三角形△ABC,
∴∠A=∠B=∠ACB=60°
∵PE∥BC,PG∥AC,PF∥AB,
∴∠A=∠B=∠ACB=∠PGD=∠PDG=∠AEP=∠CFD=60°,EP=BD,
∴△PDG为等边三角形,四边形PFCG为等腰梯形,
∴PG=DG,PE=BD,PF=CG,
∵BC=BD+DG-CG,
∴BC=PE+PG-PF.

练习册系列答案
相关题目