题目内容
【题目】用铁片制作的圆锥形容器盖如图所示.
(1)我们知道:把平面内线段OP绕着端点O旋转1周,端点P运动所形成的图形叫做圆.类比圆的定义,给圆锥下定义 ;
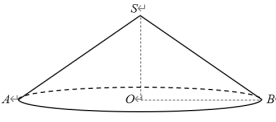
(2)已知OB=2 cm,SB=3 cm,
①计算容器盖铁皮的面积;
②在一张矩形铁片上剪下一个扇形,用它围成该圆锥形容器盖.以下是可供选用的矩形铁片的长和宽,其中可以选择且面积最小的矩形铁片是 .
A.6 cm×4 cm B.6 cm×4.5 cm C.7 cm×4 cm D.7 cm×4.5 cm
【答案】(1)把平面内,以直角三角形的直角边所在直线为旋转轴,其余两边旋转而成的曲面所围成的几何体叫做圆锥;(2)①6π;②B.
【解析】
(1)根据平面内图形的旋转,给圆锥下定义;(2)①根据圆锥侧面积公式求容器盖铁皮的面积;②首先求得扇形的圆心角的度数,然后求得弓形的高就是矩形的宽,长就是圆的直径.
解:(1)把平面内,以直角三角形的直角边所在直线为旋转轴,其余两边旋转而成的曲面所围成的几何体叫做圆锥;
(2)①由题意,容器盖铁皮的面积即圆锥的侧面积
∴![]()
即容器盖铁皮的面积为6πcm;
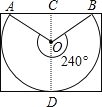
②解:设圆锥展开扇形的圆心角为n度,
则2π×2=![]()
解得:n=240°,
如图:∠AOB=120°,
则∠AOC=60°,
∵OB=3,
∴OC=1.5,
∴矩形的长为6cm,宽为4.5cm,
故选:B.

练习册系列答案
相关题目