题目内容
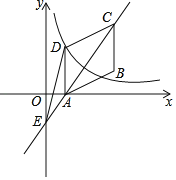
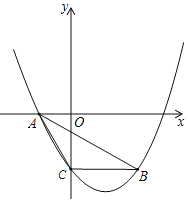
【题目】如图，抛物线y＝ax2+bx﹣4经过A（﹣3，0），B（5，﹣4）两点，与y轴交于点C，连接AB，AC，BC．
（1）求抛物线的表达式；
（2）求△ABC的面积；
（3）抛物线的对称轴上是否存在点M，使得△ABM是直角三角形？若存在，求出点M的坐标；若不存在，请说明理由．
【答案】（1）y＝
x2﹣
x﹣4；（2）10；（3）存在，M1（
，11），M2（，﹣
），M3（，
﹣2），M4（，﹣﹣2）.
【解析】
（1）将点A，B代入y＝ax2+bx﹣4即可求出抛物线解析式；
（2）在抛物线y＝x2﹣x﹣4中，求出点C的坐标，推出BC∥x轴，即可由三角形的面积公式求出△ABC的面积；
（3）求出抛物线y＝x2﹣x﹣4的对称轴，然后设点M（，m），分别使∠AMB＝90°，∠ABM＝90°，∠AMB＝90°三种情况进行讨论，由相似三角形和勾股定理即可求出点M的坐标．
解：（1）将点A（﹣3，0），B（5，﹣4）代入y＝ax2+bx﹣4，
得
，
解得，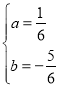
，
∴抛物线的解析式为：y＝x2﹣x﹣4；
（2）在抛物线y＝x2﹣x﹣4中，
当x＝0时，y＝﹣4，
∴C（0，﹣4），
∵B（5，﹣4），
∴BC∥x轴，
∴S△ABC＝
BCOC
＝×5×4
＝10，
∴△ABC的面积为10；
（3）存在，理由如下：
在抛物线y＝x2﹣x﹣4中，
对称轴为：
，
设点M（，m），
①如图1，
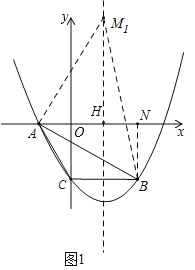
当∠M1AB＝90°时，
设x轴与对称轴交于点H，过点B作BN⊥x轴于点N，
则HM1＝m，AH＝
，AN＝8，BN＝4，
∵∠AM1H+∠M1AN＝90°，∠M1AN+∠BAN＝90°，
∴∠M1AH＝∠BAN，
又∵∠AHM1＝∠BNA＝90°，
∴△AHM1∽△BNA，
∴
，
即
，
解得，m＝11，
∴M1（，11）；
②如图2，
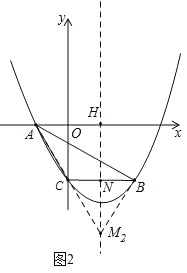
当∠ABM2＝90°时，
设x轴与对称轴交于点H，BC与对称轴交于点N，
由抛物线的对称性可知，对称轴垂直平分BC，
∴M2C＝M2B，
∴∠BM2N＝∠AM2N，
又∵∠AHM2＝∠BNM2＝90°，
∴△AHM2∽△BNM2，
∴
，
∵HM2＝﹣m，AH＝，BN＝，M2N＝﹣4﹣m，
∴
，
解得，
，
∴M2（，﹣）；
③如图3，
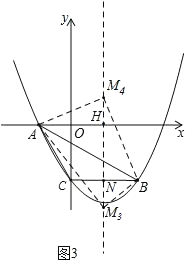
当∠AMB＝90°时，
设x轴与对称轴交于点H，BC与对称轴交于点N，
则AM2+BM2＝AB2，
∵AM2＝AH2+MH2，BM2＝BN2+MN2，
∴AH2+MH2+BN2+MN2＝AB2，
∵HM＝﹣m，AH＝，BN＝，MN＝﹣4﹣m，
即
，
解得，m1＝﹣2，m2＝﹣﹣2，
∴M3（，﹣2），M4（，﹣﹣2）；
综上所述，存在点M的坐标，其坐标为M1（，11），M2（，﹣），M3（，﹣2），M4（，﹣﹣2）．
